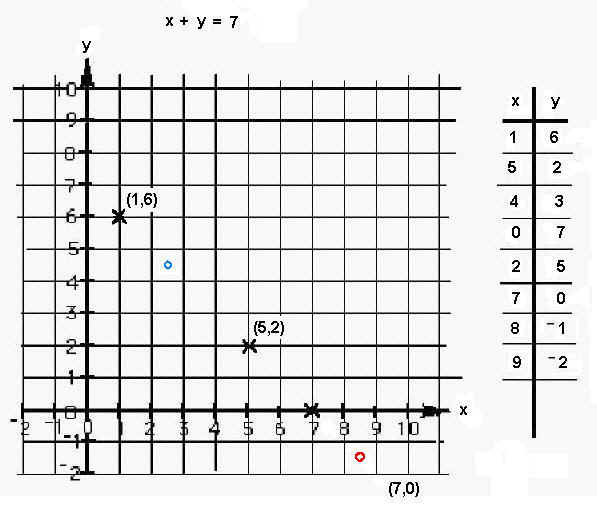
2. Patterns in graphs

Linear graphs (straight line graphs)  -see chapter 6 and Daly's graph of October 16

1. Graph x + y = 7 . Add two numbers to get 7.  1 and 6, 5 and 2, 7 and 0. We'll put these numbers in the table at the right. Then plot these points on the graph. The x-number goes along the x-axis to the right (or left). The y-number goes up (or down). See how we plot those 3 points on the graph.

Is there a pattern to the x's you've plotted? What are the two numbers for the blue point? the red point? Do these add to 7? These questions get us into fractions and negative numbers.       

2. Graph:  2x + 3 = y  What patterns do you see? Where does the 2 show up on the graph? Where does the 3 show up on the graph? (see chapter 6 and chapter 14 - slope of tangent and derivative).

non-linear graphs

3. parabola (chapter 6) The Peg Game or The Shuttle Puzzle leads to graphing a parabola. Also see Sheri's work on finding the equation of a parabola that is moved up and down, to the right and left, gets skinnier and fatter. Along the way she also changed the exponent and tried x3  = y . She saw that every parabola has a pattern of going up by odd numbers because adding odd numbers give square numbers. 1+3=4=22, 1+3+5=9=32 , 1+3+5+7=16=42 , etc. 

4. circle (chapter 6)

5. ellipse (chapter 6) & See 'math in bubbles'

6. Hyperbola - from the hinged mirrors in chapter 6

7.  Sheri works on the Tower Puzzle which leads to the graph of an exponential functions (see also chapter 6)

8. Trig functions: See Don's new , unfinished book, "Trig Functions for Young people" . See also Geoffrey's graphs of the six trig functions having used the fine IES java applet  in Japan (Don's idea).

9. Graphs of iterations in Maura's work with the function 5 + x/2 (chapter 8).  

10. Graph of the partials sums (1/2, 3/4, 7/8, 15/16, 31/32...) of the infinite series (chapter 1)

 

11. Graph 3 successive 'pieces' of the infinite continued fraction 5-6/(5-6/...) (these are hyperbolas, chapter 8).

12. Graph successive pairs of numbers of the iteration of y = 5 - 6/x (an hyperbola, chapter 8).

13. Graph of SPIRALS : a.) Below is the Nautilus shell and the polar graph of

r = et*cot(79.5*Pi/360) . The polar graph was done in Mathematica, using the following command: PolarPlot[E^(x*Cot[79.5*Pi/180]),{x,0,2*Pi}];

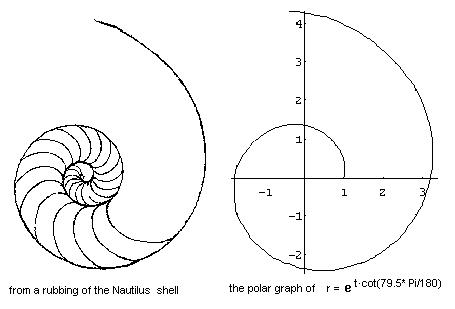
Notice that in a 360' turn of the curve at the right, it goes from 1 to about 3.2, which is same as the growth of the Nautilus shell which students have found (chapter 6).

b.) See the comparison of the spirals of The Nautilus shell, Fibonacci Numbers (Golden Mean) and The Equal Tempered Chromatic Music Scale

14. On a geoboard graph the number of nails touching a rubber band vs. the area within the shape. (see chapter 13).

15. Graph how lengths, area and volumes grow (chapter 6)

16. Graph the S.A./Vol ratio of rods to explain why rodents are nocturnal animals (chapter 6)

17. Graph y=x2 and find the area under the curve, leading to the integral (see chapter 13).

18. Graph the length of a wire vs. its resistance.

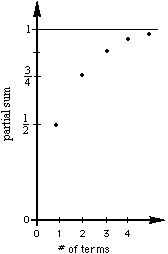
19.  Graph the ratios of consecutive Fibonacci numbers to get an infinite sequence which approaches the golden mean as the limit.

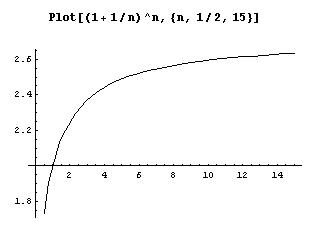
20. The graph of (1 + 1/n)n  by Geoffrey in Mathematica' . ( also see chapter 11)

21.  Graph of 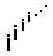 with the points connected on the complex plane

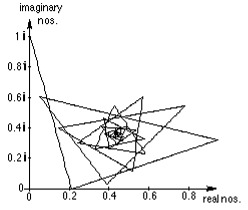
22. Graph of with the points not connected on the complex plane.

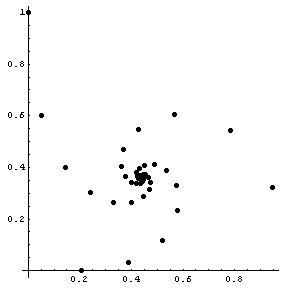
23. Graph of the sequence formed by the polypowers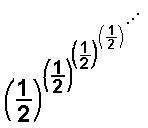

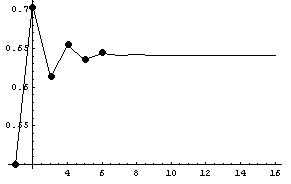
which converges to 0.64118650561396046518...

24. Graph of the limits of the sequences formed by the polypowers, like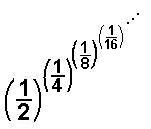

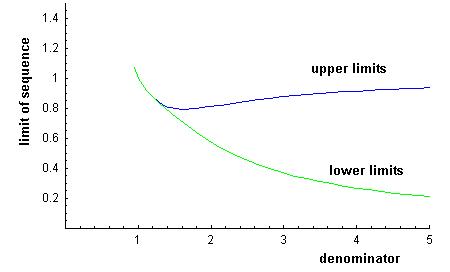
which converge to two numbers for each denominator. For the denominator equal to 2 for example, as shown above,  the sequence converges to near 0.81 and to another number near 0.57 (go up from 2 on this graph to find these two numbers).

25. Graph the length vs. width (straight line) and the length vs. area (parabola) of rectangles with perimeter of 20. (Chapter 14).

26. Graph the distance vs. time in a brick-dropping experiment (chapter 14)

27.  Graph of x=1 in 1D is a point

        Graph of x=1 in 2D is a line

        Graph of x=1 in 3D is a plane: done in David parker's DPGraph

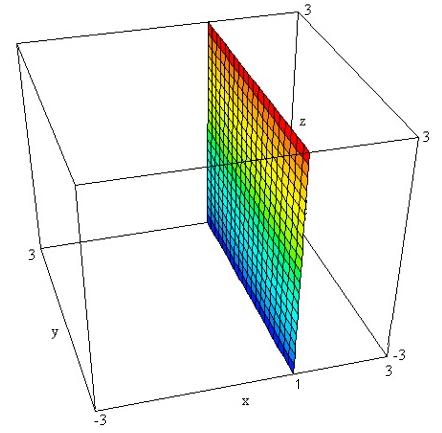
28. Move a graph, write the equation.

A. Move a graph up 2 units

Move the original graph y=x up 2 units. The resultant graph is y=x+2.

   

Move the original graph y=Abs(x) up 2 units. The resultant graph is y=Abs(x)+2.

 

 

Move the original graph y=x2 up 2 units. The resultant graph is y= x2+2

Move the original graph y=sin(x) up 2 units. The resultant graph is  y=2+sin(x).

 

 

Move the original graph y=x3 up 2 units. The resultant graph is y= x3+2.

          

Move the original graph of the circle

x2 + y2 = 4 up 2 units. The resultant graph is the circle x2 + (y-2)2 = 4.

 

 

                

 

Move the original graph of the ellipse x2/9 + y2/4 = 1 up 2 units. The resultant graph is the ellipse 

x2/9 + (y-2)2/4 = 1

     

Move the original graph of the hyperbola x2/9 - y2/4 = 1 up 2 units. The resultant graph is the hyperbola  x2/9 - (y-2)2/4 = 1

 

Move the original graph of the exponential function y=2x up 2 units. The resultant graph is the exponential function  y= 2x+2.

 

      

 

 

 

 

 

 

 

 

Back to Patterns in Mathematics
To download Don's materials
Mathman home