n.gif)
I must say that I don't know everything, and make a lot
of mistakes, in spite of what my students might believe. So I wasn't able
to give Ian a quick answer, but he and I worked very hard to solve his problem.
We started this way.
1. Simple interest. Find the amount you have in the bank after 2
years if you put in $1, at a 6% annual rate of interest. (It will always be an
annual rate of interest with all the problems below.)
The Interest = Principal * rate * time
I(2 yr) = $1 * .06 * 2 = $.12 and the
amount (A) you would have after 2 years
A = P + I = $1 + $.12 = $1.12 Notice that the interest is not added each year
to get a new principal.
2. Compound interest and 3, and 4. leading to a very important infinite
sequence. Here the interest is added after each compounding period.
Find the amount you have in the bank after 1 year, with a principal of $1, at
@6%, compounded semi-annually or 2 times per
year.
The interest earned during the first (1/2) year = I(first 1/2 year) =
$1*.06*(1/2) = .06/2 ($.03)
The Amount you have in the bank after the first (1/2) year
A = P + I =(1 + .06/2) = $1.03 which will be
the new principal.
I(2nd 1/2 year) = (1 + .06/2)* .06/2
A(after 2 (1/2)years)= P + I = (1 + .06/2) +
(1 + .06/2)*.06/2
Factoring out the term (1 + .06/2), we get
A(after 2 (1/2)years) = (1
+ .06/2)2
= $1.124 (more than the simple interest after 2 years).
What would the amount you have in the bank after 1 year, putting in $1, at 6%,
compounded quarterly (4 times per year)?
What would the amount you have in the bank after 1 year, putting in $1, at 6%,
compounded monthly (12 times per year)?
What would the amount you have in the bank after 1 year, putting in $1, at 6%,
compounded daily (365 times per year)?
What would the amount you have in the bank after 1 year, putting in $1, at 6%,
compounded 10,000 times per year?
What would the amount you have in the bank after 1 year, putting in $1, at 6%,
compounded continuously, (an infinite number of times per year)?
New things, not in my books! See the answer page to find out what Kirsten and I did with graphing and exploring (1 + .07/x)x
5. Naming ex
as an infinite series.
Using the binomial expansion from chapter 9, the first 5 terms of (A + B)n
are:
n.gif)
6. Patterns with i
7. Leading to the most exciting single mathematical statement, that contains
the 5 most important numbers in mathematics!
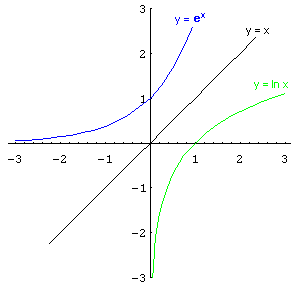 This is not
in my books, but happens regularly.When a student works on logs, as in Ch
13., I'll have them find ln(-1). Looking at the graph at the right, you can see
that ln x is the inverse function of ex
(they are mirror images of each other in the line y = x), but also there is no
ln of a negative number! Now I'll have the student find ln(-1) in Derive
and lo and behold we get ln x = i*Pi, which is not
a real number but an imaginary number... and that shouldn't show up on our graph
at the right. That means that ei*Pi
= -1 by definition of logs. Adding 1 to each side we get
This is not
in my books, but happens regularly.When a student works on logs, as in Ch
13., I'll have them find ln(-1). Looking at the graph at the right, you can see
that ln x is the inverse function of ex
(they are mirror images of each other in the line y = x), but also there is no
ln of a negative number! Now I'll have the student find ln(-1) in Derive
and lo and behold we get ln x = i*Pi, which is not
a real number but an imaginary number... and that shouldn't show up on our graph
at the right. That means that ei*Pi
= -1 by definition of logs. Adding 1 to each side we get
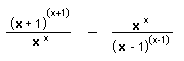 .
If x goes to infinity what does this go to? Click
here to see how Ian
figured this out.
.
If x goes to infinity what does this go to? Click
here to see how Ian
figured this out.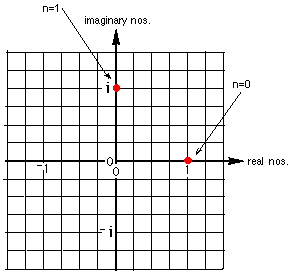
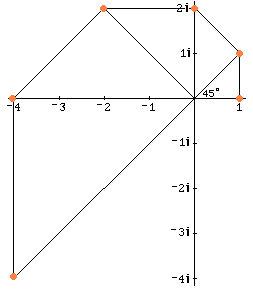
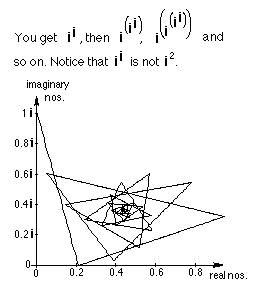
12. Back to Ian's problem.