Sample Problems from Chapter 6

Chapter 6: On Thin Spaghetti and Nocturnal Animals (function and graphs)

1. Guess my rule

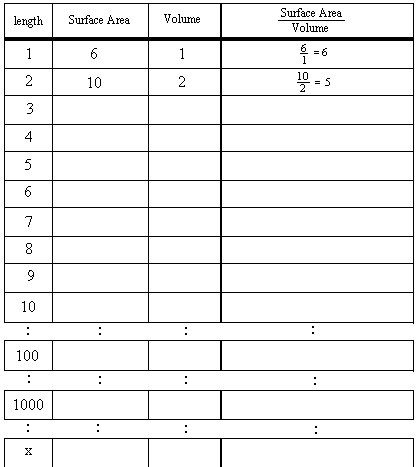
I'm thinking of a machine or rule. You give me a number (input), I put your number in my machine or use my rule on your number, then I give you a number back (output). I always do the same thing to the number you give me. Your job is to figure out how my machine works or what my rule is doing to your number.

So if you give me 1, I tell you 5. You give me 2, my machine gives out 7 and so on. We'll put the numbers in a table like this:

input output
   x        y
1        5
2        7
3        9
4      11

10 23

Can you guess my rule? Guessing the rule also means finding the output for any input number, say 100. Can you do that? Can you write a rule with x in it to =y ?
You make up a rule and send it to me.
To send a rule to Don

2. Graphing
Graph x + y = 7; that is find pairs of numbers that add to 7, that make this sentence true, then plot these pairs on the graph paper like that below:

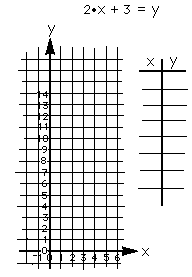
Graph 2x + 3 = y. Find pairs of number that make this sentence true. (Don't forget 0 for x)- put them in the table like that below. Look for patterns. Is there a pattern in the dots? in the numbers? What would happen if you changed the 3 to a 5? a 6? Graph these on the same graph paper. What do you see?
What happens if you change the 2 in the original equation to a 3? What do the two numbers in the equation tell you about the graph?

3. The shuttle puzzle
Now we'll get some functions from different things. The first is the shuttle puzzle.

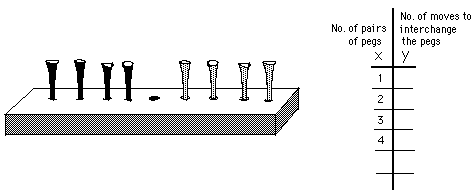
The object of this puzzle is to interchange the blue and the red pegs (golf tees). The rules are 1) you can move to a hole that's next to a peg; 2) you can jump, but only one peg and it must be of the other color, and 3) you can't move backwards. You must start with the empty space in the middle and end that way. You can use golf tees as I do or two different kinds of coins or bottle caps or pieces of colored paper as the pieces. Try it. It's not easy.

If you have difficulty, try it with 2 on each side of the space in the middle. Then you can't use the 2 holes on the outside on each side. Sometimes when a problem is hard, make up a simpler one, do that, then go to the harder one.

When you can interchange 1, 2, 3 and 4 pairs, then make a table like the one shown above. Fill in the number of pairs of pegs and count the number of moves it takes to interchange the pegs. Put those numbers in the table. Then find a rule to relate x to y. Graph these pairs of numbers.

4. The Tower Puzzle
The object of this puzzle is to move the pile of discs (4 shown here) from any one peg to either of the other two. The rules are 1) you can only move one disc at a time; 2) You can't put a bigger disc on top of a smaller one. Look for patterns.

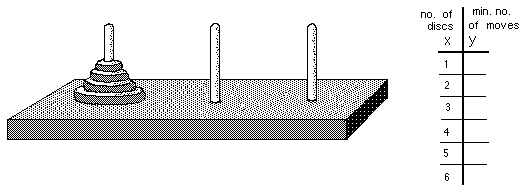
When you get good at moving 6 discs, then move the discs in the minimum number of moves. Make the table above right, and fill in the number of discs and the minimum number of moves.

Find a rule relating these numbers in the table.

Graph these pairs of numbers.

5. The Nautilus shell

Different sizes of the Nautilus Shell can be obtained from:

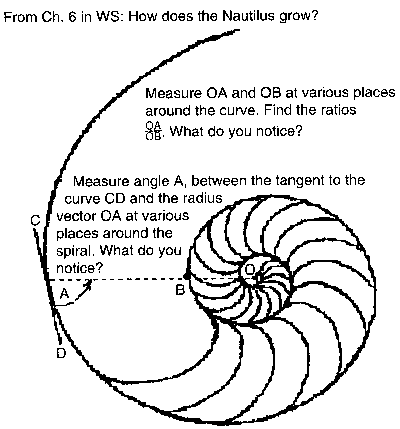
Seashell World - http://www.seashellworld.com
An environmentally educational shopping experience. Exotic sea shells, starfish, sand dollars and unique seashell novelty items. Fun for collectors and crafters alike. Dive on in!