Answers for Chapter 6 Sample Problems

1. The rule can be written various ways, like x+x+3=y and 2x+3=y

2. Below is the graph of x+y=7

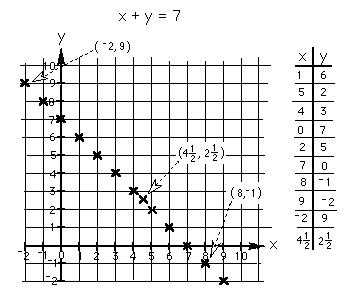
Notice, I will get young people into negative numbers and adding mixed numbers while doing the graphs. Is there a pattern to the graph? Follow the pattern. I may have to show a youngster how to write negative 1 or 2 1/2. They pick up on this quickly though!

The graphing is a very important piece of mathematics involving arithmetic (getting the numbers), algebra (the equation), and geometry (the points). Now we can ask some questions, like what could you change? How could you make the graph different? What if you graphed x - y = 2 or xy=12 ? Try these.

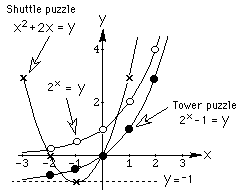
3. and 4. These are the graphs of the shuttle puzzle (a parabola), tower puzzle (an exponential function) and another to compare with these.

5. For the Nautilus shell,

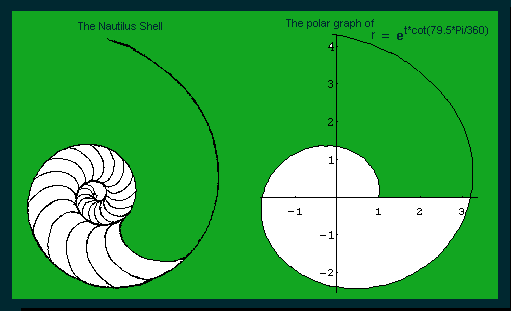the ratio of radius vectors every 360 degrees is a constant, about 3.2. My students average their mesurements and get pretty close to that (within 10%). The angle comes out another constant, about 79.5 degrees; this spiral is called an equiangular spiral because of this. A number of young people have worked on these problems of the Nautilus shell. Vickie, a 9th grader at the time, used the half-shell, and studied the volume increase from section to section. I have a full and half shell in my "Math Room". The shell is beautiful and mathematical, that's why it is my logo. The shell on my first web site page is a copy of a watercolor painting I did of the shell. The rubbing is on the left. The polar equation of the shell spiral is r = e^{t * cot (79.5*Pi/180)} The polar plot of this equation in Mathematica looks like that at right above. You can see when t =0, r =1. A 360 degree turn (t=2*Pi) gives an r of about 3.2, and the Nautilus grows at this constant ratio throughout (as mentioned above). (See Frank Land's book "The Language of Mathematics", Doubleday, 1963)

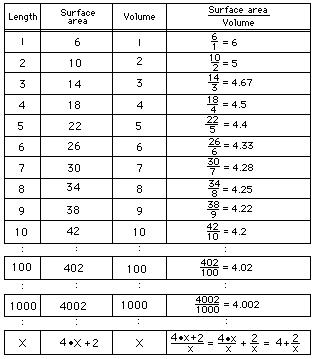Notice that in the chart above, we get an infinite sequence whose limit is 4. As the animal gets smaller, like a mouse, its SA/Vol ratio is largest (the white or smallest rod). The skin (measured by the surface area) acts to rid the body of perspiration, and the mass (proportional to the volume) is a measure of the heat production. If the mouse ran around during sunny days, it would lead to "excessive transpiration" and die. That's why rodents are noctunal animals. This ratio is also why we grate cheese before putting it on spaghetti and one person told me he likes thin spaghetti because the cheese gets on more of it!

Back to problems from Ch. 6
To order Don's materials
To choose sample problems from other chapters
See Patterns in Graphs
Mathman home