Geoboard Magic

by Maggie- a 7th grader, Patricia-a 9th grader and Paul-a 6th grader

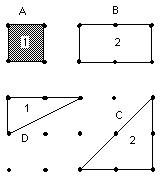
I started with making a shape with 4 touching nails on the geoboard, 1 unit of area.

I had to figure out a rule for finding the area (y) inside the shape,  with different numbers of nails  touching the rubberband (x) and the number of nails inside the figure (i).

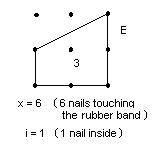
I wrote down how many units of area would be inside a figure depending on x and made a table, first for no nails inside:

I found patterns in the table, then I wrote the rule as

 x - (x+2)/2 = y

Both Patricia and Paul graphed the pairs of numbers (x, y) from their tables, for each i.

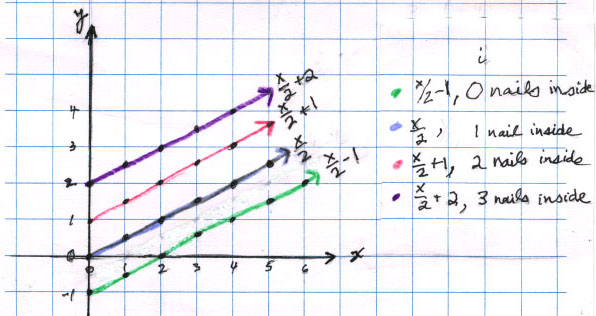
They then were able to pick off the slope (1/2 for each one) and the intercept, easily, and write the rules more simply as

     x/2 + ^-1 = y ,  when i=0

     x/2 +  0 = y ,   when i=1

     x/2 +  1 = y ,   when i=2,   and so on.

The rule with i was simple to see, because the adding number was 1 less than i. They wrote the 3-variable rule as

x/2 + i - 1 = y  (also known as Pick's theorem)

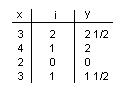
They checked this rule with the data they had and it worked!

Don helped Paul, then Maggie, make the 3-D graph of the area y in terms of x and i using the table above. The 3-D graphing board they used was a peg-board and dowel rods, marked off in units. The points were made with rubber bands. This 3-D graphing board was invented by Theo when he was in 5th grade- the same person who years later helped Don with his book "Changing Shapes With Matrices"! It looked like this:

3D graph of  the area y (vertical axis) in terms of x, the number of nails touching the rubber band (coming towards you)  and i the number of nails inside (going to the right). Check out DPGraph.com to graph in 3D on line- great!

==========================================

To other discoveries
To download Don's materials
Mathman home