
Sheri finds the Volume of a Pyramid is 1/3 the Volume of a Cube with the same base and height
Sheri built 3 pyramids out of cm cubes and tried to fit them together to make a cube, but that didn't work.
1. Sheri found 3 pyramids in the Geoblock set that did make a cube. So the volume of the pyramid was 1/3 the volume of the cube with the same base and height.
2. Then Don asked Sheri to fill a plastic square pyramid with water and see how many it would take to fill the plastic cube. It took 3 pyramids with water to fill the cube. So the volume of the pyramid was 1/3 the volume of the cube with the same base and height. These plastic pieces are from the "Volume Relationship Set" which was obtained from Ideal School Supply Company.

3. Don asked Sheri to find the ratio of the volume of a pyramid made with cm cubes to the volume of a cube also made of cm cubes, with the same base and height. The volume of the pyramids were the sum of squares, and the cubes were each a cube number. The picture of the wood pieces is shown below

Sheri's work to find the sum of the squares, the cubes, and the ratios of the volumes as a fraction and a decimal is shown below. Sheri worked very hard on these!
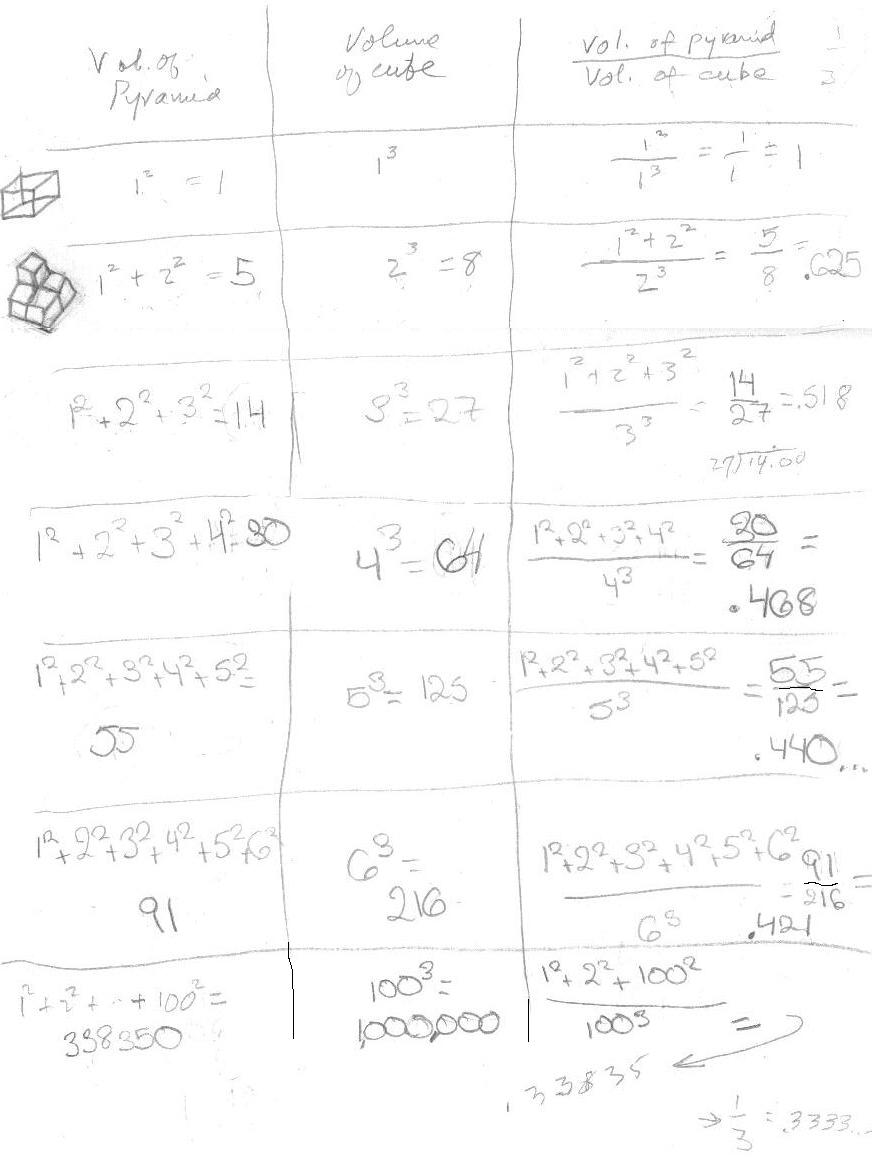
Fine work Sheri!
Using Mathematica, Don and Sheri did the first 4 below; each gives the input, then the second line is the output. Then Don did the rest after Sheri left, but he showed her what he did later.
1. below says: Find the sum of n2, from
n=1 to n=3; in other words, add 12 + 22 + 32 =
1 + 4 + 9 = 14
1.
![]()
14
2.
![]()
338350
3.
100^3
1000000
4.
![]()
0.33835
The ratios Sheri was getting form an infinite sequence
1,
5/8, 14/27, 30/64, 55/125,
91/216, .. , 338350/1000000,... or as decimals
1, 0.625, 0.518..., 0.468,
0.440, 0.421,..,
0.33835,...
This sequence is a slowly converging
sequence; it took 100 terms to reach 0.33835 and
is getting closer to 0.33333... = 1/3. Don used Mathematica to show
that the sequence really does go to 1/3.
In 5. below Don used Mathematica to find the sum of the first x squares.
5.
![]()
![]()
![]()
![]()
In 7. below Don used Mathematica to find the limit of the function above as x goes to Infinity, which is 1/3.
7.
![]()
![]()
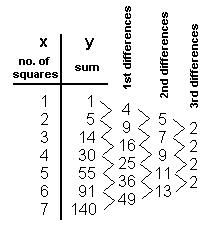
In ax3 + bx2 + cx
+ d = y , if we put x=1 and y=1, then x=
2 and y=5, then x= 3 and y=14, then x= 4 and y=30,
we get a system of 4 equations in 4 variables a, b, c, and d. The
equation number is in red.
Putting in
x=1, Eq1 = a
+ b + c +
d = 1
x=2, Eq2
= 8a + 4b + 2c
+ d = 5
x=3, Eq3
= 27a + 9b + 3c + d =
14
x=4, Eq4
= 64a + 16b + 4c + d =
30
To eliminate d:
Eq2-Eq1=Eq5=
7a + 3b + c = 4
Eq3-Eq2=Eq6=19a
+ 5b + c = 9
Eq4-Eq3=Eq7=37a
+ 7b + c =16
To eliminate c:
Eq6-Eq5=Eq8=
12a + 2b = 5
Eq7-Eq6=Eq9=
18a + 2b = 7
To eliminate b
Eq9-Eq8=Eq10=
6a=2, so a = 1/3
To solve for b, put a = 1/3 in
Eq8:
12* 1/3 +2b =5
4 + 2b = 5
b = 1/2.
To solve for c, put a = 1/3 and
b = 1/2 into Eq5
:
7*1/3 + 3*1/2 + c = 4 Multiply both sides by 6
14 + 9 + 6c = 24
6c = 1
c = 1/6
To solve for d, put a = 1/3
and b = 1/2 and
c = 1/6 into Eq1,
and we get
1/3 + 1/2 + 1/6 + d = 1, and from this
1 + d = 1, so
d = 0
If we now put a = 1/3, b
= 1/2, c = 1/6, and d
= 0 in the general case
ax3 + bx2 + cx + d = y , we
get:
1/3x3 + 1/2x2 + 1/6x
= y factoring 1/6x from each term, we get
1/6x (2x2
+ 3x + 1) and factoring the trinomial, we get
1/6x (2x + 1)(x
+ 1) which is the same as 5. above.
Now if we divide 1/3x3 +
1/2x2 + 1/6x by x3
, we get 1/3 + 1/(2x) + 1/(6x2) which is the same
as 6. above.
If we take the limit of 1/3 + 1/(2x) + 1/(6x2) as x
->Infinity, the two terms on the right go to zero, so we get 1/3,
which agrees with 7. above, and the wooden pieces, and the water filled
pyramid and cube, and Sheri's work with the wooden pieces!