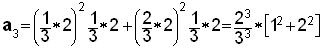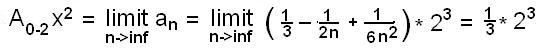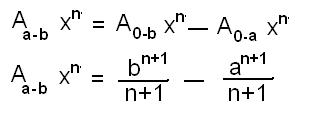The
Integral/chapter 13
1. Area on the geoboard
I start young people working on a geoboard. The geoboard I use is 1/2"
plywood with a 5 by 5 square array of nails, about 2" apart with about
1" edge. I also have "spotty" paper, with dots the same distance
apart as the geoboard so that my younger students can draw the shapes. I also
have 1/2" spotty paper for the older students.
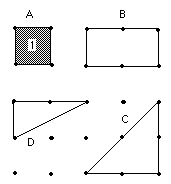
If it takes 1 can of paint to paint inside the square (figure A), how many cans
of paint does it take to fill in figures B, C, and D?
There are many investigations one can get into: Make some shapes and find how
many cans of paint it takes to paint inside them (in other words, find the area
within each figure).
How many segments can you make on this 5x5 geoboard?
How many squares can you make on this 5x5 geoboard (no diagonal sides)?
What is the area of each triangle below?
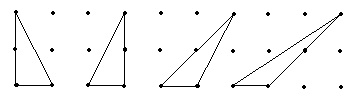
You make up questions.
2. See Katy's work
finding the area under a sine wave from 0 to p
(In
his books, Don finds the area of a
parabolic segment to find the area under a parabola, after Archimedes)
3. See Don's
program to plot points on a calculator and find the area under curves
4. Finding the area under curves
on 1/10" graph paper- and seeing patterns to learn new things!
On
August 28, 2001 Don
started working with Grace, a
6th grader in Chicago, in his Math
By Mail/Email program.
On September 22, 2001,
Grace's parents
brought
Grace and her two brothers
to Champaign to work with Don. On
Sunday, Dec.
2, 2001,
Grace's parents brought the 3 children back to Champaign to work with
Don! Grace has continued to work with Don through
February, 2002.
In
November 2001
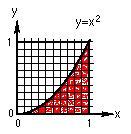
Grace started work on on the area under curves on p. 245 in Don's worksheet book. He
suggested she count the squares under the parabola y = x2
from
x = 0 to x = 1, (on the left above), then find the ratio of the number of squares under the curve to
the number of squares in the 1x1 square. Grace found the
number of squares to be about 34, so the area under the curve was 34/100. When Don asked her
what simple fraction was this close to, she said 1/3. Don had Grace write
"the area under the curve y = x2 from
x = 0 to x = 1" as A0-1
x2 = 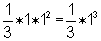 .
It would be easy to write 1 for 1*12 or 13 , but the
square is 1 by 12 = 13 and writing it
this way will show the pattern that follows. In his college math classes, Don
was often confused by the NOTATION used, which kept him from really
understanding the mathematical ideas.
.
It would be easy to write 1 for 1*12 or 13 , but the
square is 1 by 12 = 13 and writing it
this way will show the pattern that follows. In his college math classes, Don
was often confused by the NOTATION used, which kept him from really
understanding the mathematical ideas.
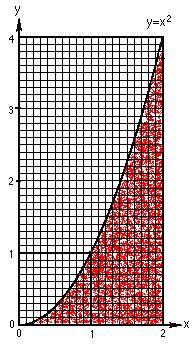
Grace counted the squares for the area from x = 0
to x = 2, above right. She found the area to be about 1/3 of the total area
(2x4). So the area under the curve y = x2 from
x = 0 to x = 2 is A0-2 x2 = 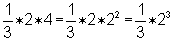 .
Looking at what she had up to that point,
.
Looking at what she had up to that point,
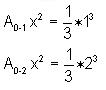
Don asked Grace what she would get for A0-3
x2 ? She immediately said
it would be
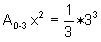 and for the
area under the curve y = x2 from
x = 0 to x = x, she predicted correctly,
and for the
area under the curve y = x2 from
x = 0 to x = x, she predicted correctly, 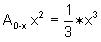 .
WOW!! The power of patterns!
.
WOW!! The power of patterns!
Then Don asked Grace to draw the line y = x and
tell him what the area under it would be from x=0 to x= 1, then 2, then
generalize to 0 to x. She sent Don the graph below as an attached file:
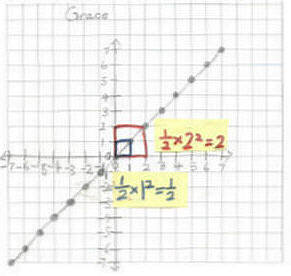
And she was able to generalize the area under the
"curve" y = x from x=0 to x=x, as 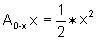 .
Looking at what she had, she was able to generalize for any function xn
, the area under the curve from x=0 to x=x would be
.
Looking at what she had, she was able to generalize for any function xn
, the area under the curve from x=0 to x=x would be 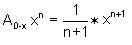 .
Using this, Don asked Grace to do the problems on p. 246 of his worksheet book. A
few days later Grace sent Don the following work as an attached file:
.
Using this, Don asked Grace to do the problems on p. 246 of his worksheet book. A
few days later Grace sent Don the following work as an attached file:

There were mistakes above, in #1, 2, 6, 11 and 12. Don sent the
following to Grace to show her that the area under y = 4 is A0-x
4 = 4x
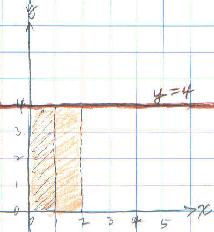
Don also sent the work below:
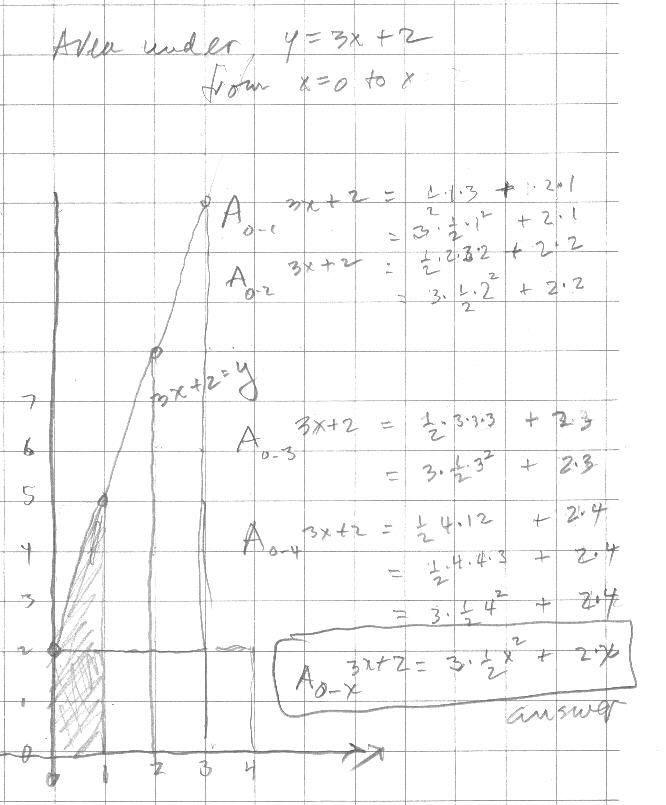
They talked about the problems she had
wrong on p.246, that of finding the area under a constant like k, which is kx0.
So A0-x
kx0=
kx.
Grace sent her corrected versions of the problems on p. 246:
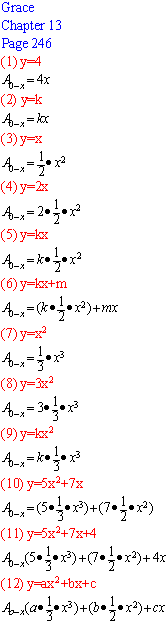
On
Sunday, Dec.2, '01 when the family returned to Champaign, Don gave Grace this
test to work on:

Grace finished her test at home and sent these answers to Don:
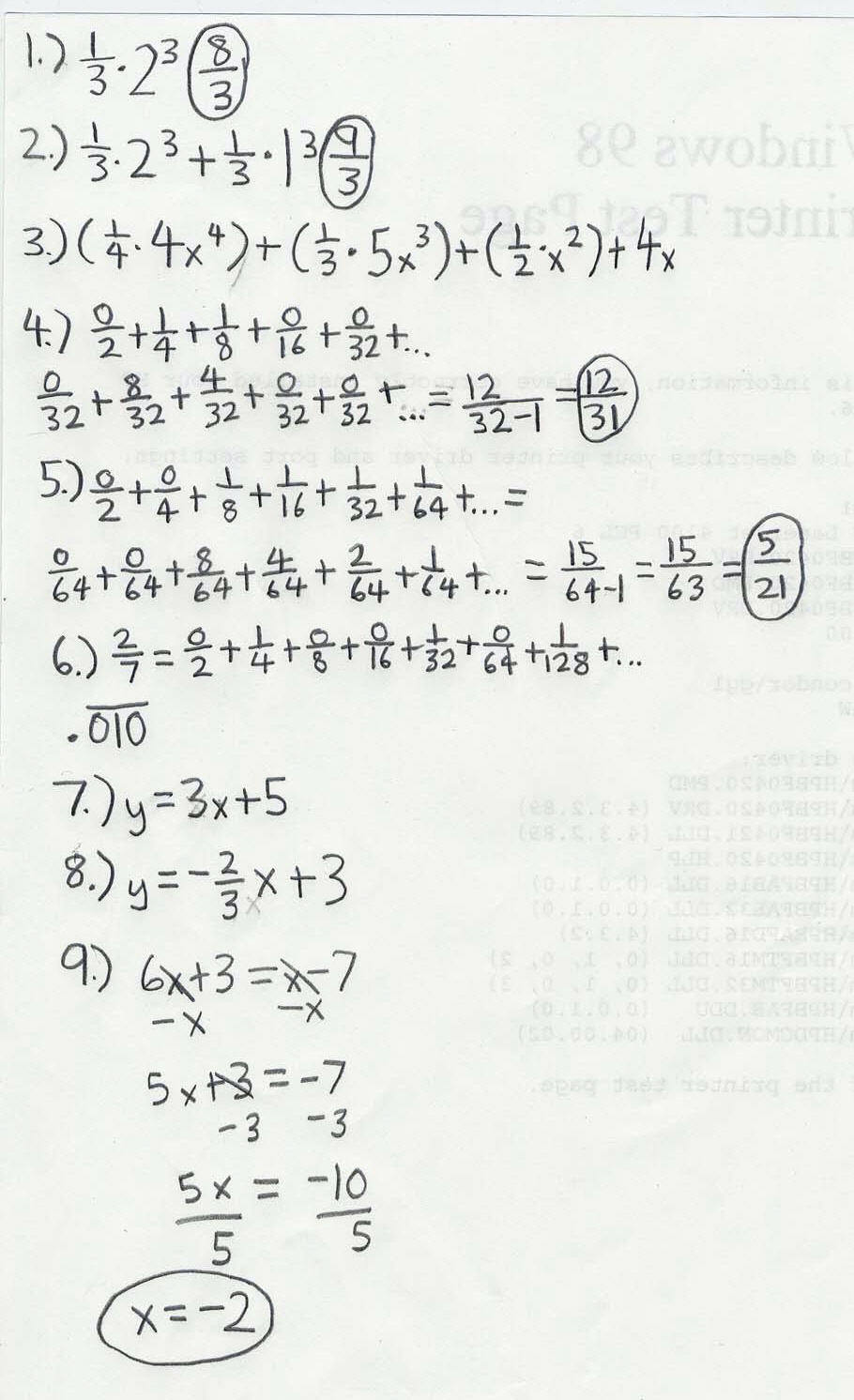
Grace is one of only a few students over the years who were able
to do #4 & #5 above. Can you figure out why one needs to subtract 1 in the
denominator?
Dec. 26, 2001 Grace sent the following scan to Don
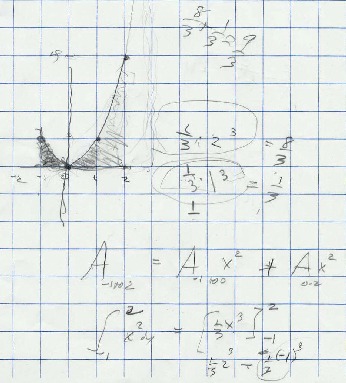
which is what they did at Don's house. This
shows how they got the answers to problem #1 (8/3) and #2 above (8/3 + 1/3= 9/3).
Don showed Grace the following was his notation and the
"normal" calculus notation where dx is the width of the rectangles
shown below:
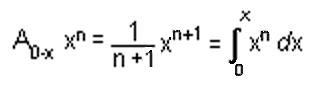
In March 2002, see what Grace writes (unsolicited) about
teaching !
As a teacher I need to try new things, do mathematics
myself, and look for ways to get my students into more difficult concepts, but
at their level. I treat each student as an individual; I do different things
with different students. And I don't wait until I completely understand
everything about an idea (which I don't think is possible anyway) before I'll get a student doing it-- that way I learn
things along with my students. It's also why I encourage them to do things
different ways. It makes teaching and learning enjoyable.
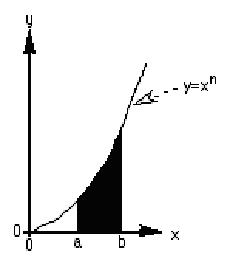
5. Area under curves using rectangles
Now comes a new
problem, that is, the curve is the same, but the method of finding the area
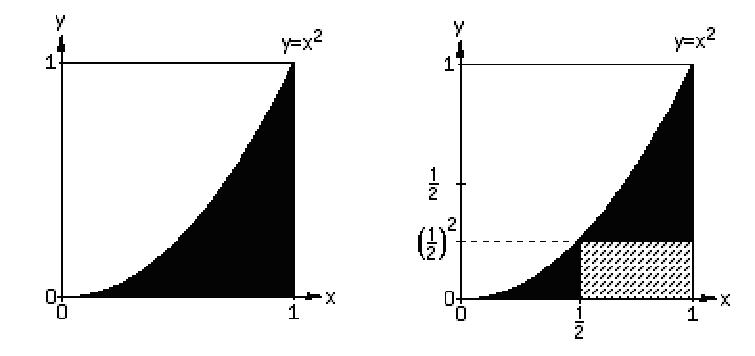
under it, is different. Find the area under the curve y = x2 (the
dark area below), from x
= 0 to 1. This time we'll make
rectangles (hatched), then find the
area of these, get a sequence of partial sums as we
make the width of the rectangles smaller, then we'll find the limit
of this sequence, which will be the area we want. The area of the hatched
rectangles will approach the area under the curve. We'll start with a1
and a2 below.
Notice that the height of the rectangles are square numbers because the curve is
y =
x2.
The hatched rectangles will have an area of the height times the width.
a1
=
0
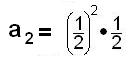
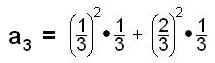
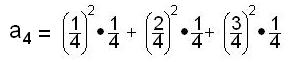
a1
= 0
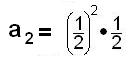
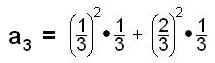
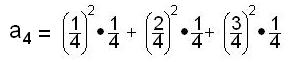
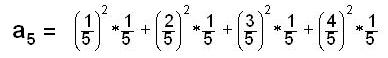
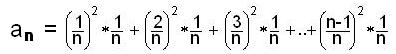
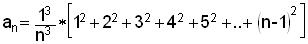
In the Vol
of Pyramid/Vol of Cube Don shows how he finds the sum of the first n
squares;
the sum of the first n-1 squares is 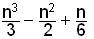
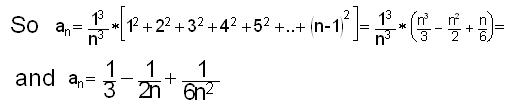
The area under the curve y=x2
, from 0 to 1 is
.gif)
because as n-> inf both the terms 1/2n and 1/6n2
->0. The 1/3 is the same as Grace got
above.
Again writing this as 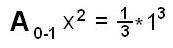 is
important because it shows
is
important because it shows
that the area is 1/3 of a 1x12
rectangle, which is what Sean, Matt, and Grace got.
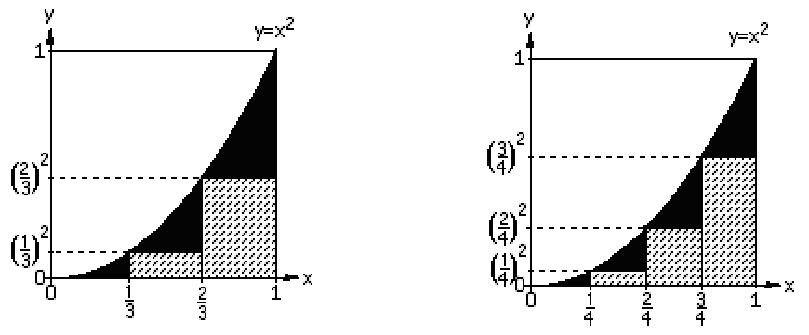
Could you find the area under the
curve y=x2 , from 0 to 2,
using the rectangles under the curve? Find a1,
a2, a3,
and a4, using the
diagrams below. a3 is
given below the diagrams.
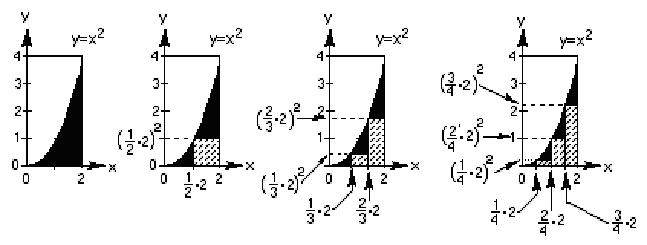
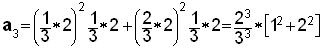
Generalize to an,
then find the limit of an
as n-> infinity.
This becomes 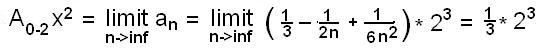
Can you now find the area under y=x2
from 0-3, 0-4, 0-x?
Now find the area, using rectangles, under the
curves x0, x1
, x3
. x4
, .. xn
|
From what we've done so far, what do you think
would be the area under the curve xn
from x=a to x=b?
Just the difference between
the areas under the curve
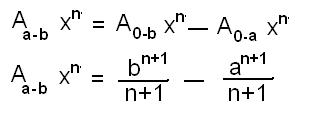
|
 |
6. Two problems:
a. Find the area under x2
from 0 to 1.
b.
Find the ratio of the volume
of a pyramid / the
volume of a cube with the same base and height
What
do you notice about the answers above?
7. a. Logarithms,
and
b. logs as area under
the curves 1/x and 1/(1+x), and as infinite series
At age 11,
Ian realized that he could go down, starting with y= x4 ,
taking the derivative until he got 0, or go up, taking the integral! He used the following notation to show this:
y
-2' =
x6/30
y
-1' = x5/5
he started here y 0' =
x4
y
1' =
4x3
y
2' =
12x2
Ian's notation for the 2nd derivative was y 2'
,
normally
written as y"
y
3' =
24x1
y
4' =
24
y
5' =
0
Jonathan
was Don's student years ago and has made Don's A Map To Calculus ' clickable. See
Jonathan's blog at
http://www.technicalmisery.com/2011/02/cylinder-fun.html
for
finding the volume of a cylinder.




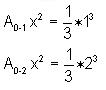
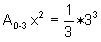 and for the
area under the curve y = x2 from
x = 0 to x = x, she predicted correctly,
and for the
area under the curve y = x2 from
x = 0 to x = x, she predicted correctly, 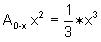 .
WOW!! The power of patterns!
.
WOW!! The power of patterns! 
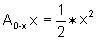 .
Looking at what she had, she was able to generalize for any function xn
, the area under the curve from x=0 to x=x would be
.
Looking at what she had, she was able to generalize for any function xn
, the area under the curve from x=0 to x=x would be 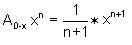 .
Using this, Don asked Grace to do the problems on p. 246 of his worksheet book. A
few days later Grace sent Don the following work as an attached file:
.
Using this, Don asked Grace to do the problems on p. 246 of his worksheet book. A
few days later Grace sent Don the following work as an attached file:


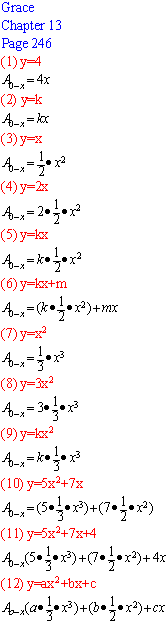

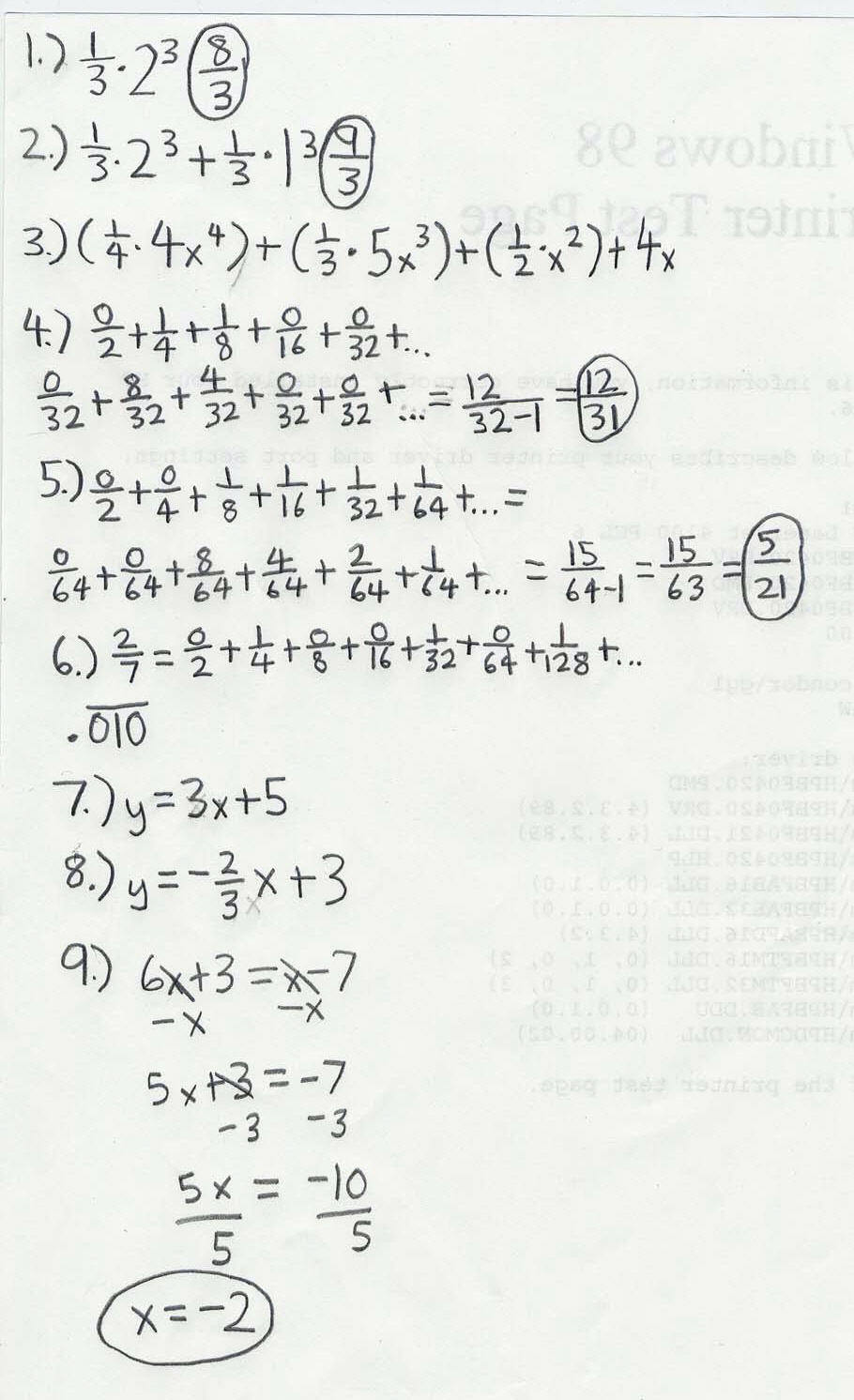

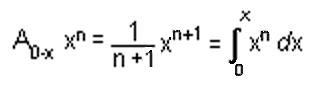

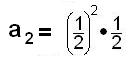

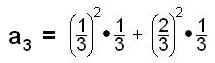
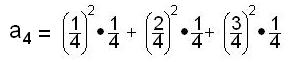
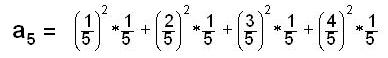
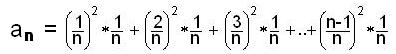
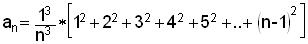
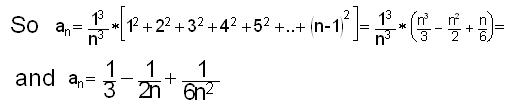
.gif)