Plotting points on a calculator to find the area under curves/chapter 13

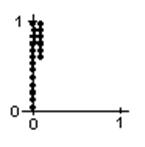
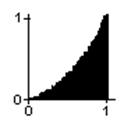
I was browsing through a Scientific American "Computer Recreations" article in which it looked like they were filling in squares on a computer screen. I asked myself "Could I do that on our programmable graphics calculator?" After a couple of hours of trying things and making mistakes (I was never very good at programming), I was able to plot points on the screen to make a 1x1 square starting on the left, below. I counted the number of points plotted, and this number was a measure of the area of the square. I wrote the program so it was possible to change the upper level of the points that are plotted, because the next thing I would wanted to do was to plot the points under a parabola, like x2, or x3, or a quarter-circle, a sine wave, or whatever. Very exciting! The figure on the right was the area under a parabola, from x=0, to x=1; as predicted, this area came out to be very close to 1/3.

                

 My progam to plot the points to make a square:
  • On the calculator
  • 1)Window -2.35, 2.35, 1, -1.55, 1.55, 1
  • 2) 0 -> x (sets left side)
  • 3) 0 -> N (counts points in both cases)
  • 4) Lbl 3
  • 5) 1 -> y (sets top of figure)
  • 6) Lbl 4


  • 7) Plot x,y (plots the point)
  • 8) 1+N -> N
  • 9) y-.07 -> y (moves next pt. down)
  • 10) y >or= 0 then goto 4 (sets bottom)
  • 11) x+.07-> x (moves next pt. to rt)
  • 12) x &ltor= 1 then goto 3 (sets rt end)
  • 13) "N = ": N Disp (displays no. of points)
  •     in Basic
  • 10 FOR X=0 TO 9 STEP .1
  • 15 N=0
  • 20 FOR Y=0 TO 81
  • 30 T=150 + 9*X
  • 40 V=150-Y (30 and 40 adjust for 
    the way pts are plotted on the 
    computer screen)

     

  • 50 PSET (T,V)
  • 60 N = N+1
  • 90 NEXT Y (moves next point up screen)
  • 100 NEXT X (moves next point to right)

     

     

  • 110 PRINT N
  • 120 STOP

Running this program fills in a 1x1 square; the number of dots varies with the calculator or computer. On my calculator I got 400 points. To change the program to plot the points under a parabola y = x2 from 0 to 1, replace the 1 in line 5 with x2. In the basic program change statement 20 from 81 to x2. I got the picture on the right with N=133. So the area under the curve y = x2 from 0 to 1 was 133/400, very, very close to 1/3 = 133/399, which is the integral of x2, from 0 to 1!! Needless to say, this was very exciting! I showed it to everyone- teachers, students, and parents. [N.B.- you might have to adjust the programs for your computer or calculator].

The following is a flowchart to help write the programs above.

Well now, if I don't have a calculator or computer can I still do this? SURE! I started doing this on 1/10" graph paper.


Finding the area under curves on graph paper: (From the scan of Sean's graph below I

added the colors and some lines to make things more readable) 
Matt, a 7 year old, counted the squares under y = x2 from x = 0 to x = 1. He counted 32 squares, and 32/100 of the 1 x 1 blue square below as the area. Byron, a 10 year old recently doing this, counted 42 squares and I told him to go back and do it again and be more careful. He too came up with 32. I asked Matt what simple fraction was close to this.

He said 1/3; I wrote this as 1/3*1*12 or 1/3*13.



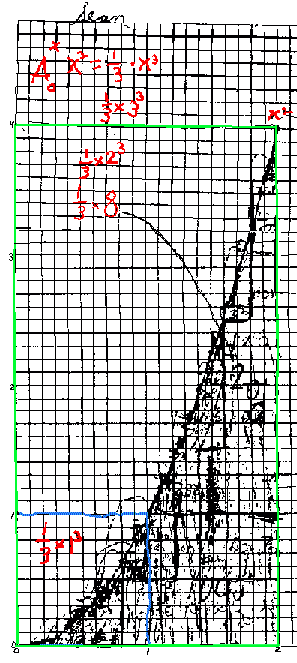
From 0 to 2 he correctly predicted 1/3 of the 2x22 rectangle or 1/3*23 (the green rectangle above) as the area under the curve y = x2 from x = 0 to x = 2.
Sean counted approximately 279 squares in going from 0 to 2, but was satisfied this was close enough. He figured there are 20*40 = 800 little squares in the 2x4 green rectangle and the area should be 1/3 of 800 or 266.66... which is close to 279. The notation I used on his graph I now have changed to and use A0-1 (x2) = 1/3*13. Then the area from 0-2 he wrote as A0-2 (x2) = 1/3*23. Writing the area this way instead of 1 and 8, makes it possible to see a pattern. I always want my students to look for patterns. Writing the answers different ways often helps to see the pattern.

What would you predict would be the area from 0-3? 0-4? 0-n? 
How about finding the area under the curve y = x3 from 0-1? 0-2? 0-n?... Look for patterns! 

See theintegral