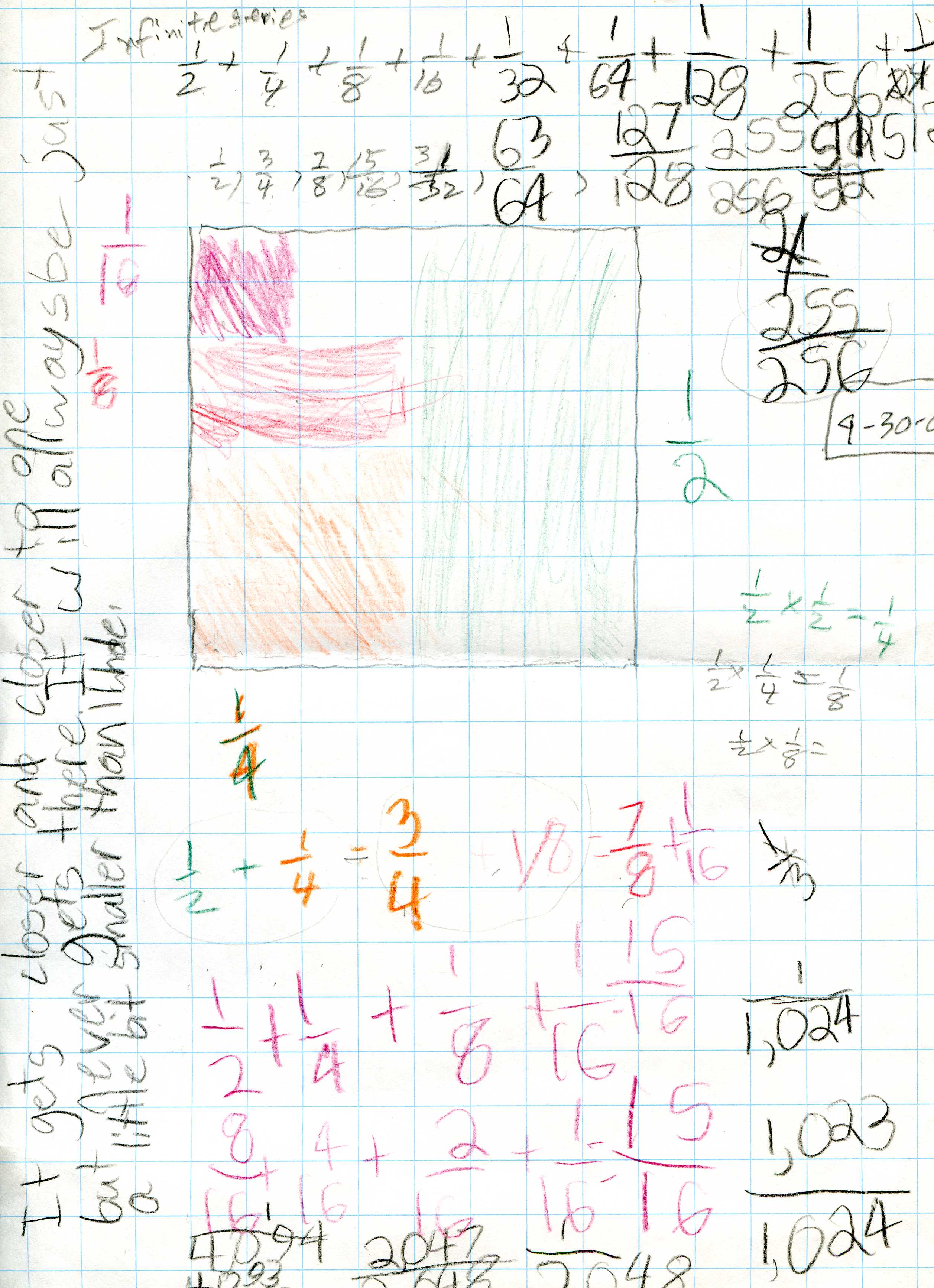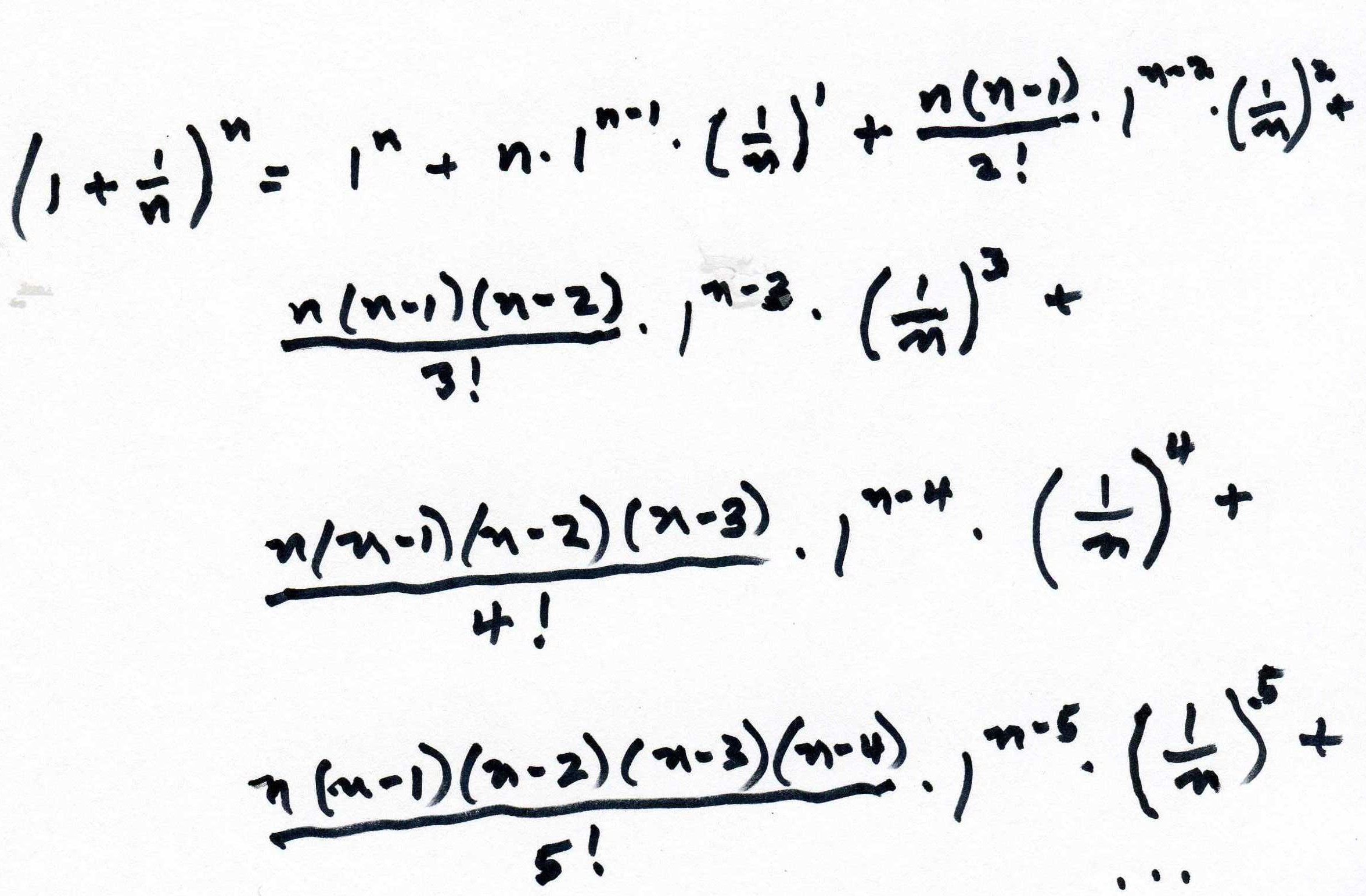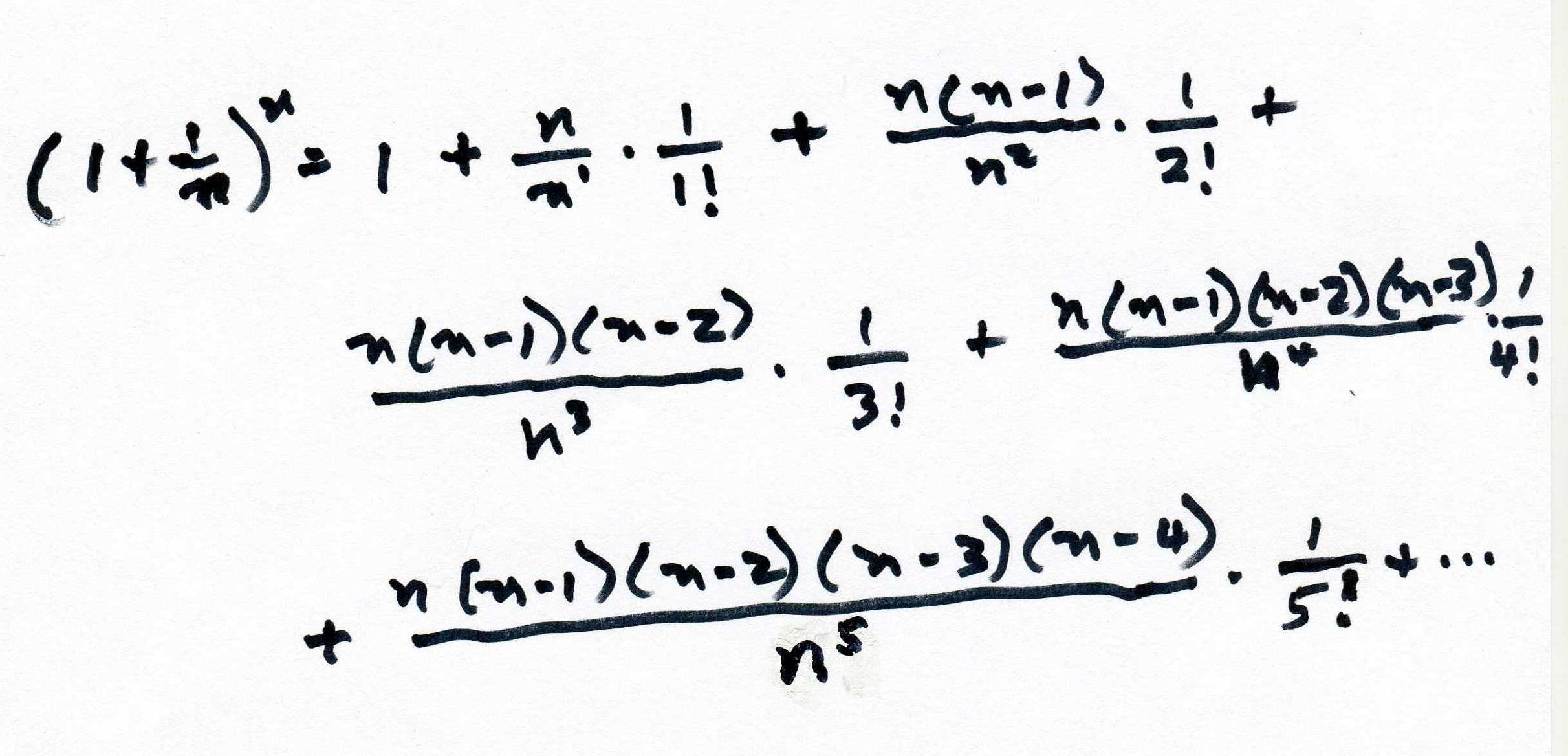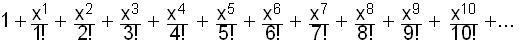Discoveries about  INFINITE SERIES

By Katy, 10th grader

BACKGROUND

Mr. Cohen had previously shown me an interesting property of infinite series.  He started by having me find the sum of the infinite series ' + ' + 1/8 + 1/16 + 1/32 ' He suggested that I use a picture and color in a half, and then add a fourth and then add an eighth, a sixteenth, etc. until I found what the infinite series approached.

The picture showed that the infinite series approaches 1. 

Mr. Cohen next gave me the problem 1/3 + 1/9 + 1/27' This problem is a little trickier to show using diagrams, it's easier to use decimals (in Excel) to explain this problem:

As you can see, this chart shows that the infinite series approaches .5 or '  . No matter how many terms you add, the series will not reach .5. It would only reach point five if you could keep adding into infinity.

The next problem was ' + 1/16 + 1/64 + 1/256'

As you can see, each time another term is added, the infinite series gets closer to .333' or one third.

Mr. Cohen then asked me to figure a pattern for 1/n + 1/n^2 + 1/n^3 + 1/n^4'..

' + ' + 1/8 + 1/16 + 1/32 '             approached 1/1

1/3 + 1/9 + 1/27'                              approached 1/2

' + 1/16 + 1/64 + 1/256'                 approached 1/3

The rule seemed to be that 1/n + 1/n^2 + 1/n^3 + 1/n^4'.. will approach the limit 1/(n-1).

In Mr. Cohen's book Calculus by and for Young People '--Worksheets one of the problems caught my interest. It involved sharing 2 cookies between 3 people using 'special scissors' -- scissors that could only cut the cookies into two equal pieces. If the special scissors were used once on each cookie, then there would be 4 pieces and each person would get one piece, or ' a cookie. The remaining half-cookie would be cut with the scissors into two pieces that would each be one fourth. Since three people cannot evenly share two pieces they would not receive any of the newly cut pieces. Another way to put it would be that each has person received '  + 0/4 so far. The two left over pieces (which were each one fourth) would be cut again, so there would be four pieces that were each a eighth of the whole. Each person would get one of the new pieces, so they would have '  + 0/4 + 1/8. The remaining eighth would be cut again. The two new pieces would each be a sixteenth of the whole. Since two pieces cannot be divided between three people, each person would not receive either of the new pieces. That means that each person receives ' + 0/4 + 1/8 + 0/16. This pattern would continue, with the cookie being cut forever and each person receiving ' + 0/4 + 1/8 + 0/16'

MY DISCOVERIES

Another way to write ' + 0/4 + 1/8 + 0/16 + 1/32'

 is ' + 1/8 + 1/32'

OR it can be written as 1/2 + 1/(2^3) + (1/2^5) ' I wondered if there was a rule that said what 1/n  + 1/(n^3) + 1/(n^5)' , the sum of the odd powers, approached.

 I already knew that ' + 1/(2^3) + (1/2^5) ' approached 2/3, so I next I tried to see what 1/3 + 1/(3^3) + 1/(3^5)' would approach.

As the table shows 1/3 + 1/(3^3) + 1/(3^5)' approaches .375 or 3/8

Next I tried to see what 1/4 + 1/(4^3) + 1/(4^5)' would approach

 It approaches .26666666666666666666... or 4/15

So far, I'd learned:

 '  + 1/(2^3) + (1/2^5) '                   approaches 2/3

1/3 + 1/(3^3) + 1/(3^5)'                    approaches 3/8

1/4 + 1/(4^3) + 1/(4^5)'                    approaches 4/15

This suggested the series 1/n  + 1/(n^3) + 1/(n^5)' approaches the limit  n/(n^2 ' 1)

Since I'd found that

1/n + 1/n^2 + 1/n^3 + 1/n^4'.. approaches 1/(n-1)                              and                  

1/n  + 1/(n^3) + 1/(9^5)'approaches  n/(n^2 ' 1)

I wanted to find a rule for the limit of 1/n + 1/(n^4) + 1/(n^7) + 1/(n^10)+...

I guessed that it would be n/(n^3 '1)

I tested my rule on the series ' + 1/16 + 1/128 '

I thought it would approach 2/(2^3 ' 1) or 2/7, but 2/7 is .2857142. I used the computer to find out what fraction the infinite series was approaching, and it gave me 4/7, or .5714285

My new guess for the rule for 1/n + 1/(n^4) + 1/(n^7) + 1/(n^10) +... was (n^2)/(n^3 ' 1). I tested this idea on 1/3 + 1/81 + 1/21897'

I thought that it would approach (3^2)/(3^3 ' 1) or 9/(27-1) or 9/26 or .3461538

When I added the first six terms of the series

I found that my guess was correct.

I took a look at the three rules I'd learned so far:

1/n + 1/n^2 + 1/n^3 + 1/n^4'.. approaches 1/n-1

1/n  + 1/(n^3) + 1/(n^5)'approaches  n/(n^2 ' 1)

1/n + 1/(n^4) + 1/(n^7) + 1/(n^10)' approaches (n^2)/(n^3 ' 1)

I noticed a very definite pattern. In the first series the numbers in the denominator did not skip any power as they went up (n^1, n^2, n^3'.) and the rule was (n^0)/(n^1 ' 1).

In the second series the numbers in the denominator skipped one power each time (n^1, skip n^2, n^3, skip n^4, n^5, skip n^6') and the rule was (n^1)/(n^2 ' 1)

In the third series the numbers in the denominator skipped two powers each time (n^1, skip n^2 and n^3, n^4, skip n^5 and n^6, n^7') and the rule is (n^2)/(n^3 '1)

This shows that a general rule is that if you have an infinite series with 1 in the numerator,  and y is the number of powers skipped in the denominator; then the rule for the limit of  that series will be  (n^y)/(n^(y+1) - 1)"

Fine work Katy!

Links to other infinite series in Don's works and 

student discoveries

Anna L., a 4th grader, does some fine Mathematics

INFINITE SERIES  (chapter 1 in Don's worksheet book)-Anna worked on the infinite series for a few weeks:

  She colored in pieces of an 8x8 square to show this infinite series:

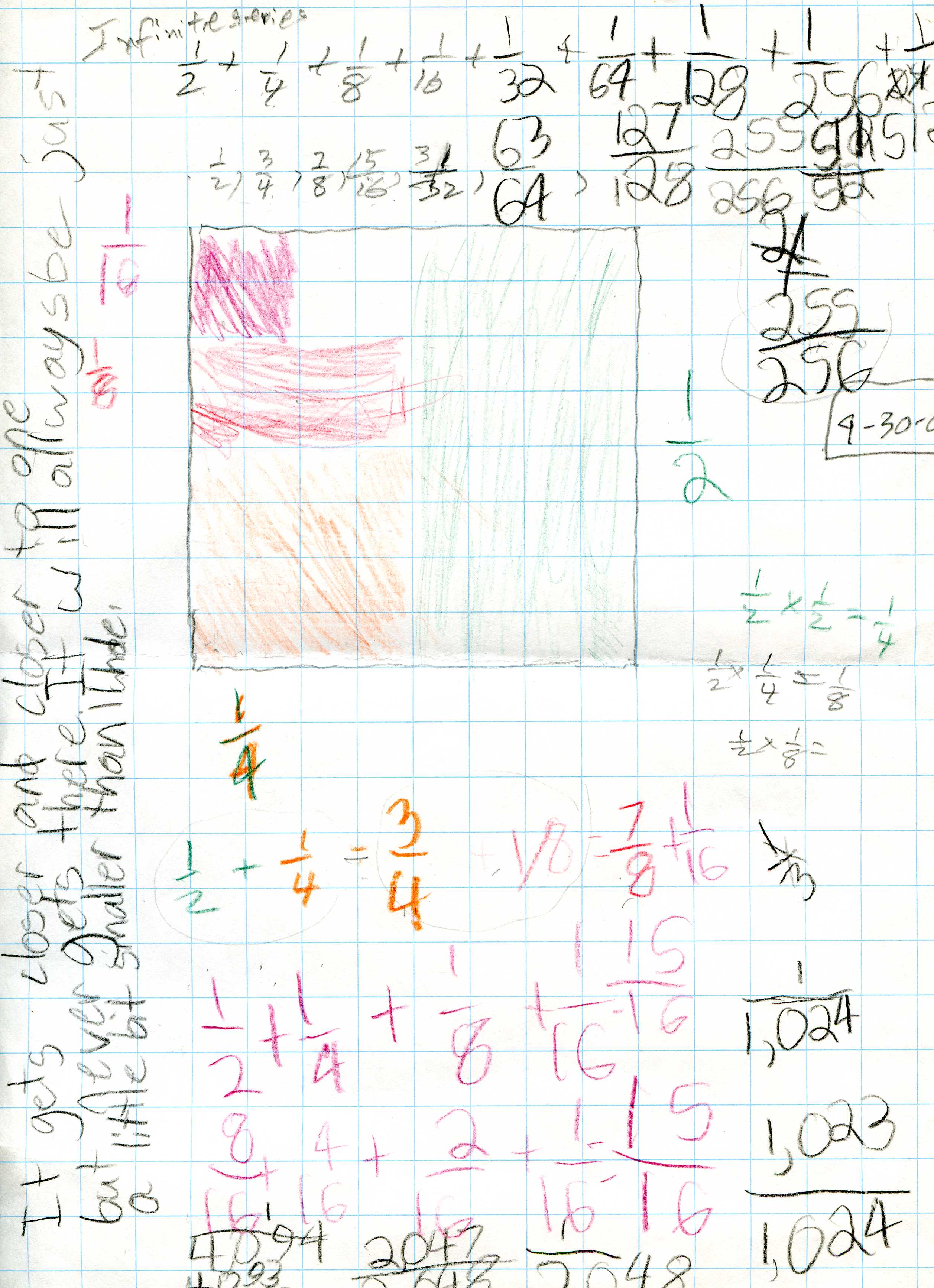
On the left side above, she wrote about what is happening "..It gets closer and closer to one..".

Don asked Anna to graph the partial sums 1/2, 3/4, 7/8, 15/16, ... vs. # of terms added for the infinite  series 1/2 + 1/4 + 1/8 + ... below:

   She saw that the graph of the partial sums 1/2, 3/4, 7/8, ... approaches 1, which she said about the picture above that. To see what other exciting things Anna L. has done, click here.

Jocelin, a 3rd grader,  finds patterns in the infinite series

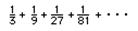
Kaitlin shares 3 cookies between 5 people, 3 ways (one was an infinite series from a trimal!)

ErinK Don asked Erin to do 1/3 and 1/3 of 1/3, and 1/3 of 1/3 of 1/3 and so forth, but  instead Erin did 1/3 + 1/3 of what was left, each time, which turned out very interesting.

Lizzy & Cheryl , 7th graders, find the sum of 1/n + (1/n)²+ (1/n)³+ (1/n)⁴+ (1/n)⁵+ ... and  A/B + (A/B)² + (A/B)³ + (A/B)⁴ + (A/B)⁵  +... and use Jeff's method for finding this last one also.

Geoffrey generalizes Q/N + (Q/n)² + ...  and writes a program with his Dad in Mathematica

How far does the ball travel if it is dropped from 6 feet and bounces back 2/5 of the distance when it hits the ground each time? (problem comes from Chapter 1).

Change this infinite repeating decimal  0.343434... to a fraction (by using an infinite series).  

TaraT invented a new infinite series

A program in Basic to do the cookie-sharing using Brad's method and get the bimal (the numerators only, the denominators are powers of 2).

• 10 c=0
• 20 INPUT T
• 30 INPUT B
• 40 PRINT INT(T/B);
• 50 n = T - B*INT(T/B)
• 60 n = n*2
• 70 c = c + 1
• 80 IF c>10 THEN STOP
• 90 IF n>B THEN GOTO 110
• 100 n<=B THEN GOTO 150
• 110 x = 1
• 120 PRINT x;
• 130 n = n - B
• 140 GOTO 60
• 150 x = 0
• 160 PRINT x;
• 170 GOTO 60
• 180 end

Ian finds the sum of the this infinite series: 1 + a + a² + a³ + a⁴ + a⁵ + ... = 1/(1-a), then shows that  Infinity = ^-1 in Chapter 3

Leibnitz series (chapter 1): the sum of the reciprocals of the triangular numbers.

^{The harmonic series      what do you get for the sum?}  

Don shows that the limit of the infinite series 2/5 + (2/5)² + (2/5)³ + (2/5)⁴ + ... equals the area within a triangle

Area of triangle= limit of infinite series, applet done by Lori and Don - you need to download free, geogebra and Java

Binomial Expansion of (1-x)^-1  =  an Infinite series 

The binomial expansion of (1 + 1/n)ⁿ :

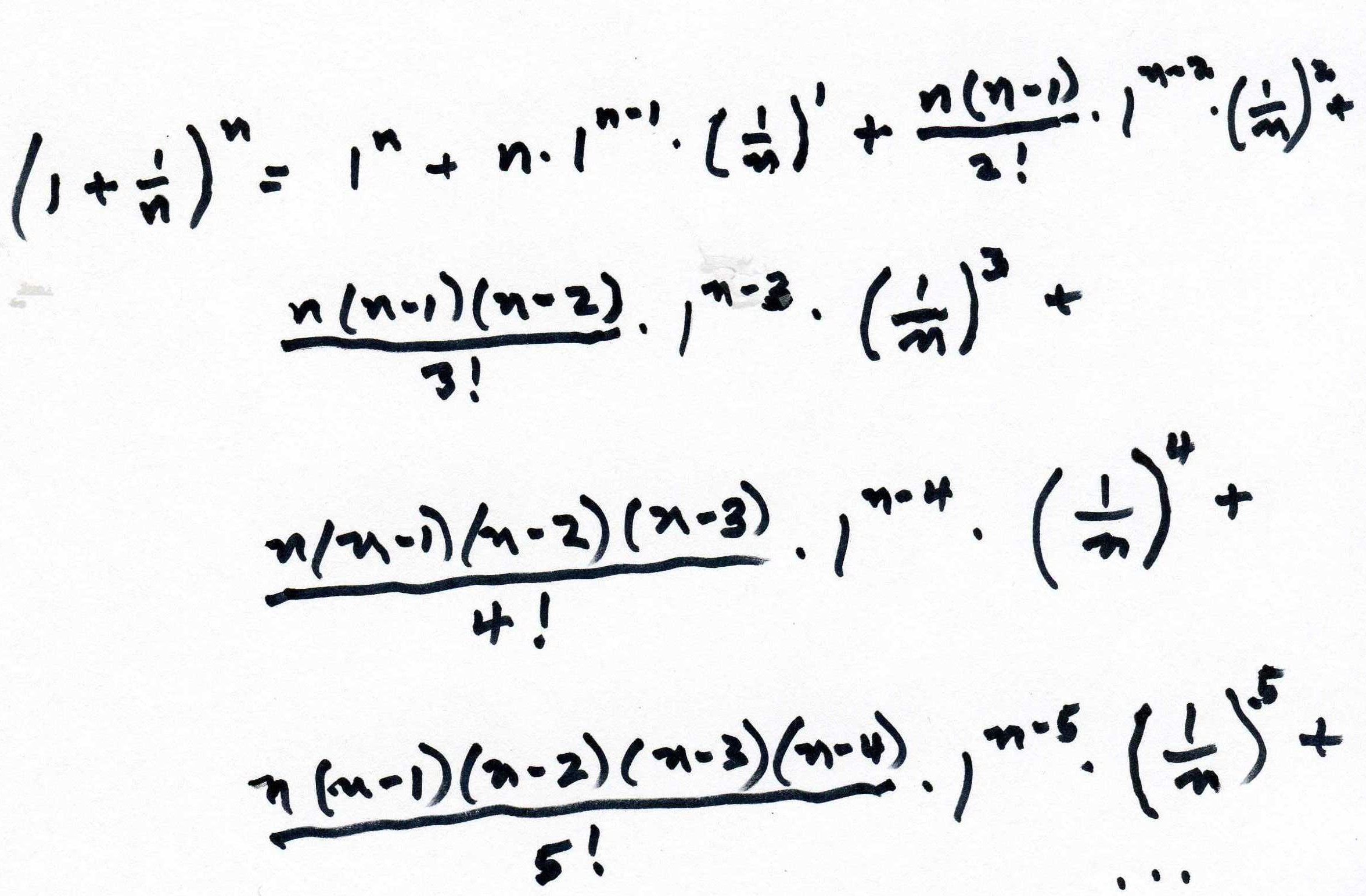
1^{any power}  = 1, and interchanging n⁵ and 5! and all terms like that, we get

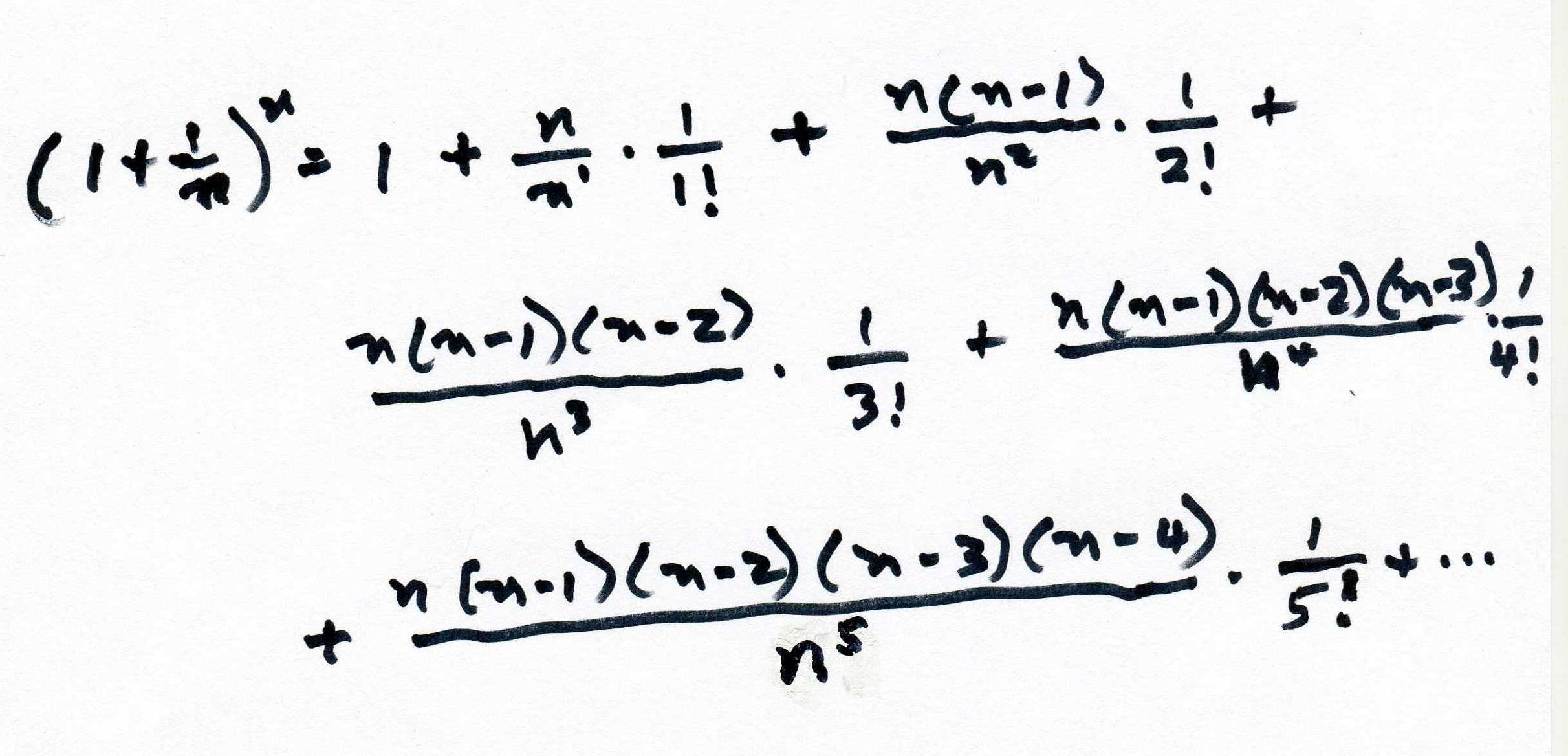
Then take the limit of (1 + 1/n)ⁿ as n->infinity, we get

The Infinite series for e^x  = 

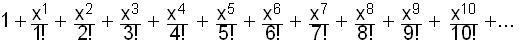
Infinite series for e^ix (put ix -> x above) = 

⁼ 

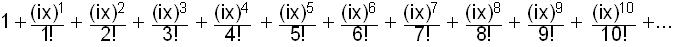(remember the powers of i⁰ = 1, i¹ = i, i² = ^-1,  i³ = ^-i, i⁴ = 1, ...)

^{eix = =}

separating the real terms and imaginary terms and factoring out i, we get

^{eix =}

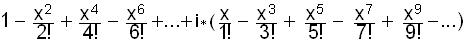
AND

the infinite series for cos x is

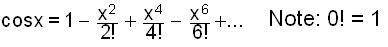
^{infinite series for sin x is} 

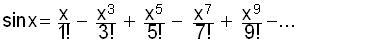AND

                                           ^{eix = cos x + i*sin x}

^{An infinite series is used to find the area under a parabola, using Don's version of how Achimedes would do it, in Chapter 13 (the infinite series is 1/4 + (1/4)2 + (1/4)3 + (1/4)4 + (1/4)5 +... not surprising)}

Cookie-sharing (Brad's method-special scisssors) -chapter 2

Patterns in the area of squares

Convergent, divergent, limit of ('goes to')

As a name for a simple fraction (chapter 1)

As a name for an infinite repeating decimal (chapter 1)

Pi See Chapter 11 , e^x See Chapter 11,  sin(x) and  cos(x) in Chapter 11.

Don's interpretation of Archimedes' method to find the area under a parabolic segment (chapter 13). Katy finds the area under a sine wave from 0 - Pi

To find the area under curves (chapter 13)

To find the area and perimeter of the snowflake curve (chapter 4 and Emily)

To find the area and perimeter of the Serpinski curve (chapter 4)

To write an infinite repeating decimal as an infinite series and a fraction, like 0.373737... or 1.3027027027... (chapter 1).

KatieR's pattern in the partial sums of the infinite series 1/2 + 1/4 + 1/8 + 1/16 ...

Tim finds a new way to write the nth term of an infinite geometric series.