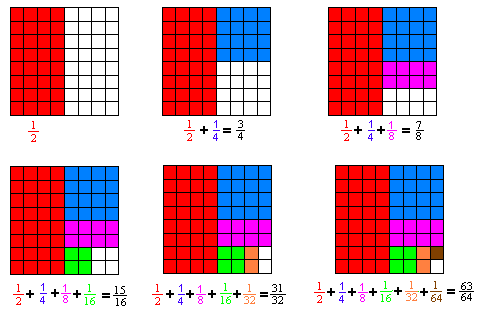
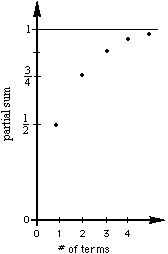
The partial sums are 
and the graph of the first 5 is shown at the left.
The fractions we're adding: they are getting smaller. The tops are 1. The bottoms are doubled each time or they are powers of 2. 8= 2^3, 16 = 2^4, and so on.
The partial sums: They are getting bigger. If you add the top and bottom, you
get the top number in the next partial sum. The top number is always 1 less than
the bottom number. The bottom number is always a power of 2. We can write the
nth partial sum as (2^n - 1)/2^n. Some people say that there is always one of
the fraction left over, so the nth partial sum can be written as 1 - 1/(2^n). I
say the infinite series 
goes
to 1. (As n-> infinity, 1/(2^n) ->0, so 1-1/(2^n)->1 and
(2^n-1)/2^n -> 1 and mathematicians say the limit of these is 1; and the
limit of this series is 1).
(With young people I don't introduce the word limit right away).
[Barbara, Don's friend, July, 2001, asked Don what this curve was, a parabola? Don thought about this and realized it was an exponential function y = 1-1/2x. Good question, Barb!]
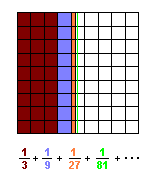The infinite series 
goes to 1/2. The partial sums are 
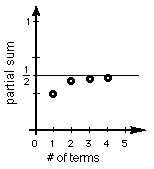Lucas, a 6th grader, saw that
each partial sum is 1/2 of the fraction less than 1/2; for example, 1/2 -
(1/2)x(1/81) = (40 1/2)/81 - (1/2)/81 = 40/81 , then proceeded to generalize
this to 1/2 - (1/2)x(1/3^n) and as n -> infinity, (1/3^n) -> 0 and the
expression 1/2 - (1/2)x(1/3^n) goes to 1/2.
).
A program to find
In Basic (prints the first 20 partial sums):