Nanako, from Japan, changes a graph, but keeps the equation the same, HOW?!

Don started Nanako on graphing linear equations, specifically x+y=8  below,  because she is 8 years old. She picked up the plotting points quickly and proceeded to find pairs of numbers with negatives numbers, like 9+^-1= 8 and plotted (9,^-1) and (10,^-2) and (^-1,9). Then Don asked her to get the numbers for a point half way between 2 others, and proceeded to get (3 1/2, 4 1/2) and she knew that 3 1/2 + 4 1/2 = 8.

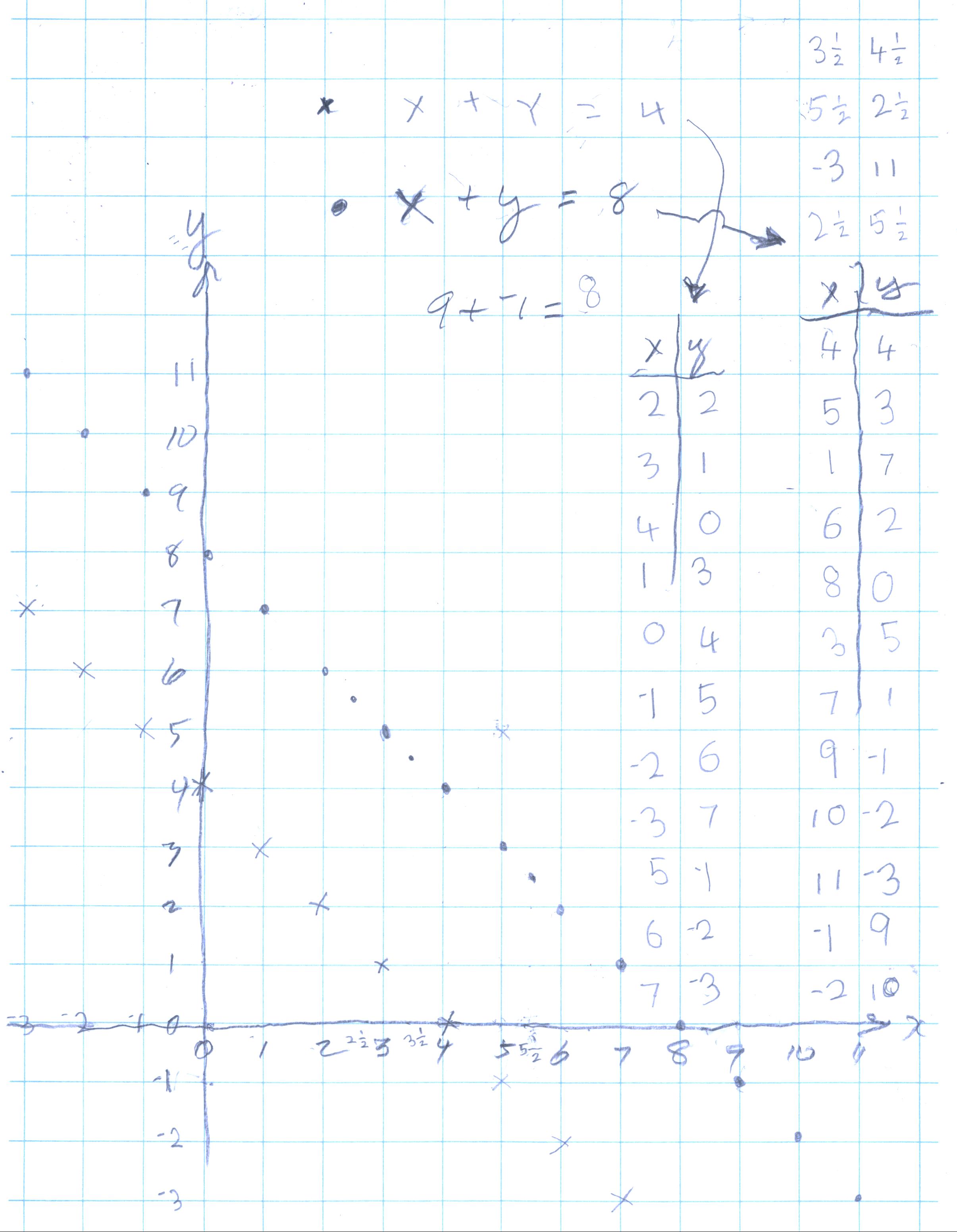
Then Don asked her to change one thing in the equation, like x+y=4; what would the graph look like? She said it would be smaller (whatever she meant, I wasn't sure). She proceeded to graph this equation above. Don told her that the lines will never meet and are parallel. Again Don asked her to change something in the equation. This time she said she would try to get a line that went like this / instead of like \. She said she would move the y-axis to the right, and she proceeded to make the negative numbers on the x-axis go down to the right, and the positive numbers get bigger to the left!!! Don had never seen anyone do this before, he was very excited! Here is her graph using the same equation:

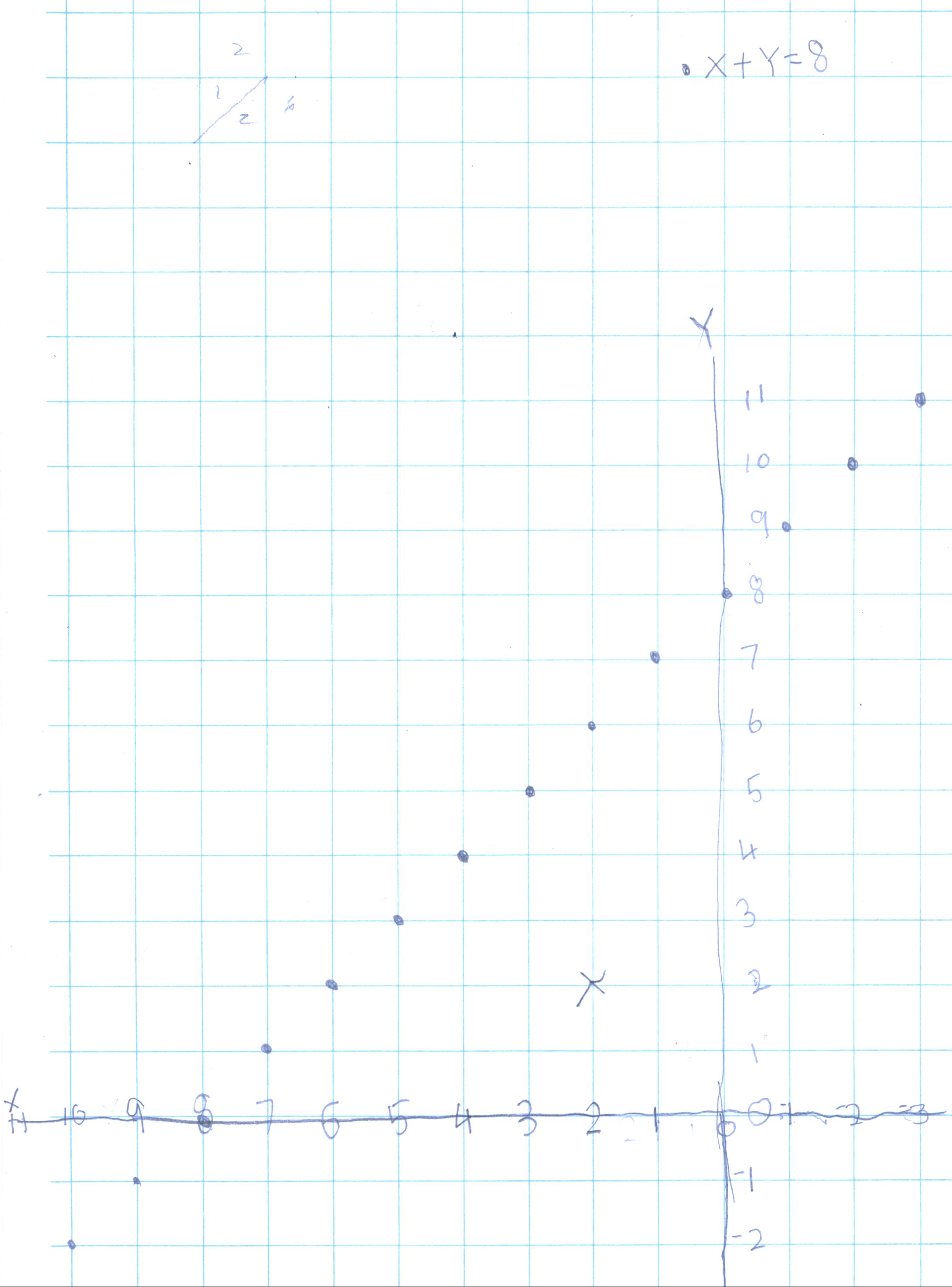
That's exactly what she was trying to do! WOW!! Don asked Nanako how she came to do this, and after thinking about that, she said, "it just popped into my head"!

Don went over the fact that a point like (2,2) marked with the x, was not on the line and the pair of numbers do not make the sentence true, 2+2 = 8 is False. Only the pairs of numbers that make x+y=8 true, will be on that line.