ON A CIRCULAR GEOBOARD, Michael, a 9th grader & Christie,
getting ready for college, find the angle formed by 2 chords intersecting within
a circle (not at the center).
On the circular geoboard, Michael and Christie found the number
of degrees between the nails (24 nails, 15 degrees apart), then found the number
of degrees in a central angle= the number of degrees in its intercepted arc.
Then they found that the number of degrees in an inscribed angle is 1/2 its
intercepted arc.
Then I gave them the problem of finding the angle x formed by 2 chords EB and
DA, intersecting within a circle at F(not at the center). This was a very
exciting event!
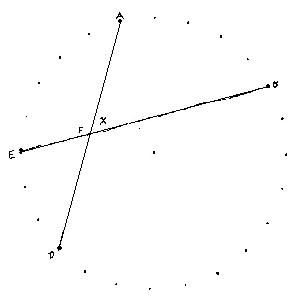
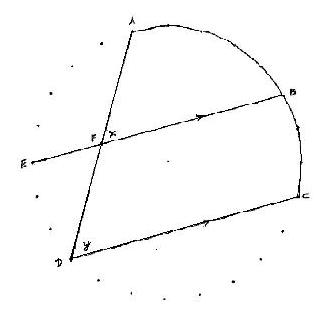
They drew a chord DC parallel to EB (same number of degrees in the arcs ED and
BC). By corresponding angles, angle x = angle y. Angle y is an inscribed angle
whose intercepted arc is AC = 120 degrees. Therefore angle y=1/2 of 120 = 60
degrees, and then angle x = 60 degrees!
I thought that was a very unique and simple way of finding angle x...don't you
agree?
One could show that this is equivalent to what we read about in most geometry
books- try that.
To other discoveries
To download
Don's materials
Mathman home
