Jamie, an 8^th grader, solves the quadratic equation

x² - x - 1 = 0,  by iteration, and he and Don write a program to do this on a TI84 Plus

Here is how Jamie solved the equation:

                      x² - x - 1 = 0
                                     add x and add 1 to both sides              

                                         x²  = x + 1

                                                                              take the square root of both sides
                                          ^{x =}

Don showed Jamie how to iterate the right side:

^{Jamie chose 3 to put in for x:   = 2;}

So we have the start of a sequence 3, 2, ..  Now put 2 in for x to get  _{=  ,}

So our sequence now is 3, 2, , ..  Now put  in for x, and keep doing that forever. Don and Jamie wrote the program below to do this, on a TI 84 Plus calculator:

: input x

: display x

: 1->N       [this is a counter to keep track of how many times to iterate the function]

: Lbl 4      [this tells where to come back to from the goto statement]

: disp     [prints out new x]

:  -> x      [puts the new value of x in for x]

: N+1 -> N   [inceases the counter]

:if N>10      [tests to see if its done more than 10 iterations-actually there   are 11 numbers printed, the original guess, plus 10 more]

:  stop     [if N>10, program stops]

: goto 4   [if N is not >10, the calculator goes to Lbl 4, to repeat the cycle]

The 11 numbers printed out (to 8 decimal places chosen) if you choose 3 for the original guess are:

3.00000000, 2.00000000, 1.7320505081, 1.65289165, 1.62876998,  1.62134820, 1.61905781, 1.61835034, 1.61813174, 1.61806420, 1.61804332

Don explained to Jamie that the limit of this infinite sequence (the number it is approaching) is an important number in mathematics, the Golden Mean (sometimes called the Divine Proportion). Jamie knew the quadratic formula, and we used that to solve the original quadratic equation:

x² - x ' 1= 0

The solution to the general quadratic equation

ax² + bx + c = 0  is

In our case a = 1, b = - 1 , and c = - 1, then substitute these in the formula

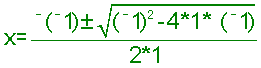  simplifying

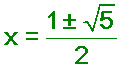
This gives the 2 answers for our quadratic equation x² - x ' 1= 0

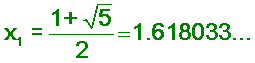
and

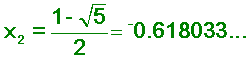
The 1.618033...  is the Golden Mean and shows up in nature where the Fibonacci numbers are found (see ch.7 in Don's books for the Fibonacci numbers and ch.8 for other ways to solve a quadratic equation by iteration).