Don's new discovery about infinite series!

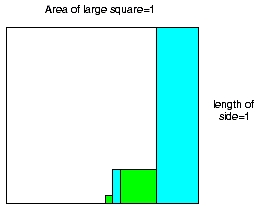
The figure below will work for any infinite geometric series. We'll look at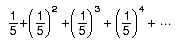



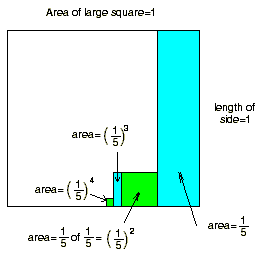
Notice some things in the diagram above: The odd powers of 1/5 are tall rectangles, and the even powers are squares, which makes sense. Don flipped the picture above about the axis of symmetry of the big square..

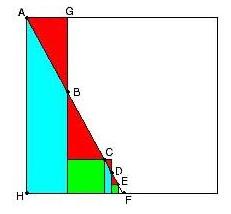If we now draw a line which connects point A, the upper left corner of the big square, to the upper right corner of each of the smaller squares at C and E, we hit the base of the big square at F and form the triangle AFH.

This triangle will have an area which will be the sum of the infinite series!!


Try to figure out why this works yourself.
To other discoveries
To download Don's materials
Mathman home