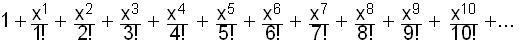
Infinite series for e^ix , Cos x and  Sin x

From the binomial expansion of (1+x/n)ⁿ and finding the limit of the infinite series, as n->infinity, we get 

the infinite series for 

       ^{ex =} 

Substitute ix->x   

to get the Infinite series for 

^{eix =}  

Remember the powers of i: i⁰ = 1, i¹ = i, i² = ^-1, i³ = ^-i, i⁴ = 1, ... and look for patterns!

 ^{eix =}

Factor out the i, and separate the real terms from the imaginary terms,

^{eix =}

So

^{eix =}

^{The infinite series for cos x is}

^{The infinite series for sin x is}

^{Substituting cos x and sin x in eix  above, we get}

  ^{eix =  cos x + i*sin x} 

^{where x is an angle in radians}

^{From this we can get eiPi  = cos Pi  + i* sin Pi = -1 + 0 = -1 and}  

e^i*Pi +  1 = 0

again the 5 most important numbers in mathematics in 1 statement!

See chapter 11