
Number of ways to make a train as long as the yellow rod (using Cuisenaire Rods' to get Pascal's triangle)

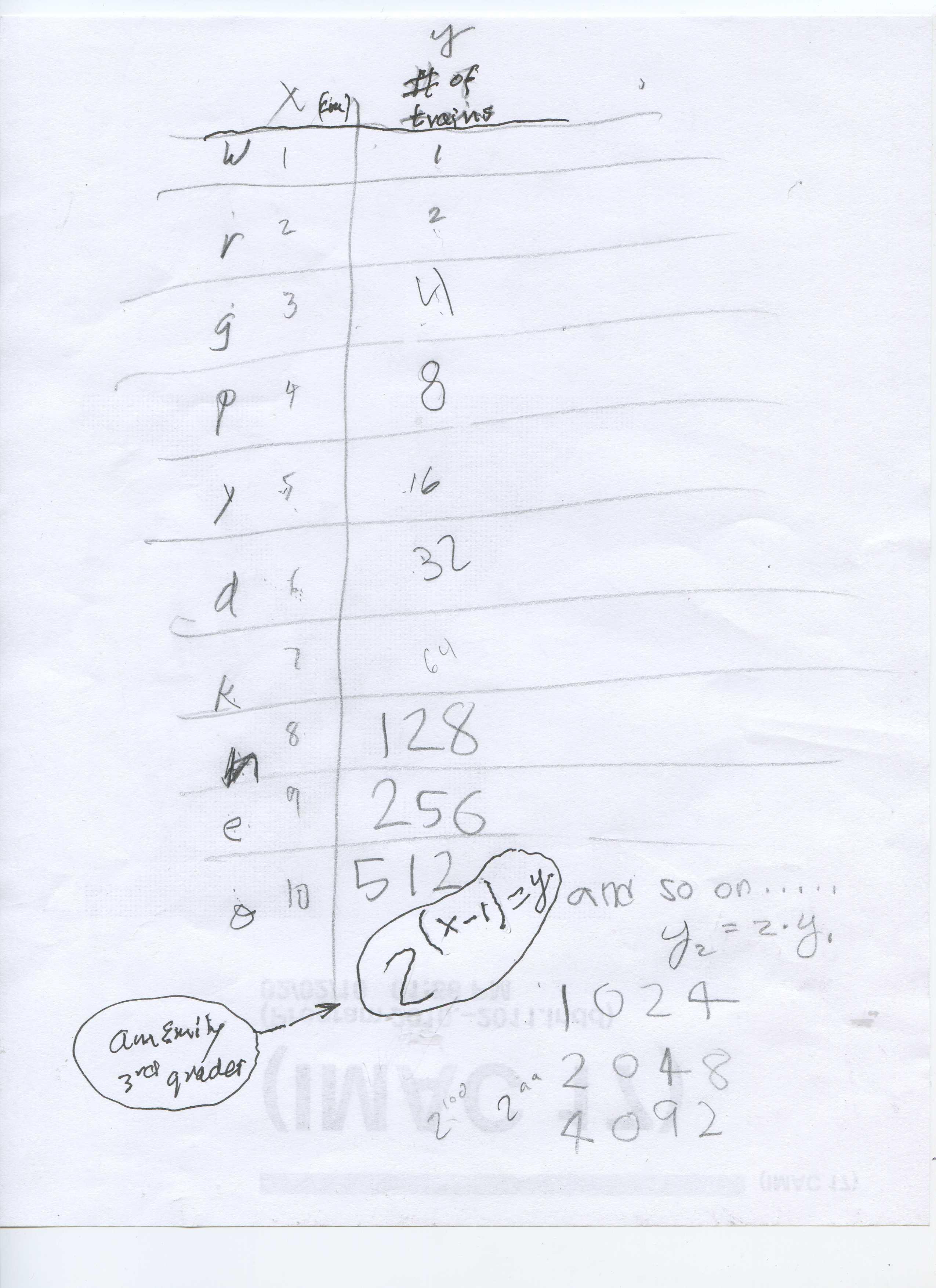
On 4-29&30-10, Don asked 5 students-Shaleen, Anushka, AnnEmily, Townes and Kashuv- to each take a rod- red, light green, purple, yellow and dark green. They were asked to make trains as long as that rod. Townes started with the orange and soon AnnEmily told him he would need 512 trains! Don had them enter the number of trains in this table below. Many of them came up short and Don suggested they look at other ways to make the trains. AnnEmily saw that the y-numbers were doubling, so Don wrote her recursive rule as y2= 2*y1.; then he showed her that she could write these as powers of 2. She ended up with the function rule 2(x-1) = y to get the number of trains from the length of the rod.
Don asked Shaleen to put the trains for the yellow rod in order of the # of cars in the train..1-car tains, 2-car trains, and so on. he came up with the following. Don took a picture of Shaleen's trains, but because of the flash, distortion and persective, Don felt the need to draw in the cracks to enhance the picture:
At this time, Don started making the patterns on graph paper to show Pascal's triangle- he used Shaleen's 1 4 6 4 1 above, and others filled in their row. Don also had Shaleen work on (a+b)2 by using the distributive property, and (a+b)3, to see the coefficients were these same numbers they were getting, and left him to find (a+b)4 . Anushka wrote her purple trains using letters, like- w,w,r in her book, without Don saying anything! A couple of very exciting sessions!