Sample Problems from Chapter 7
Chapter 7: The Fibonacci Numbers, Pineapples, Sunflowers and The
Golden Mean
See Tara's (Don's granddaughter!) story
"A Quest For The Sacred Golden Pineapple, Pine Cone and
Artichoke"
and the diorama made
by Don's son Brian.
1. Mathematics from a pineapple- infinite sequences, limit of a sequence,
ratios, fractions, and decimals:
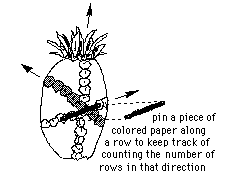 Buy a
pineapple. (This is one of those lessons that you can really eat up!) Look
carefully at the rows on it. There are three directions of rows. Count the rows
in each direction. This takes a while to see because every pineapple is not
perfect. If you are careful, you can do it! What do you find?
Buy a
pineapple. (This is one of those lessons that you can really eat up!) Look
carefully at the rows on it. There are three directions of rows. Count the rows
in each direction. This takes a while to see because every pineapple is not
perfect. If you are careful, you can do it! What do you find?
The number of rows in the three directions on the pineapple are 8, 13, and
21. These are 3 consecutive Fibonacci numbers. How can you get from the
first two to the third one? Can you write the 4 Fibonacci numbers before these?
And the four that are larger?
These Fibonacci numbers form an infinite sequence: 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, ...
Write a program to get these Fibonacci numbers.
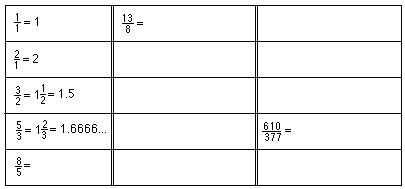
Find the ratios of larger to smaller of each consecutive pair of Fibonacci
numbers (do about 15 of these). Write the answer to each ratio as a mixed number
and a decimal. For example 5/3 = 1 2/3 = 1.666... Fill in the chart below:
Graph this sequence, the number of the term on the x-axis, the value on the
y-axis. I'm calling the first term 2 on the graph shown. Look for patterns.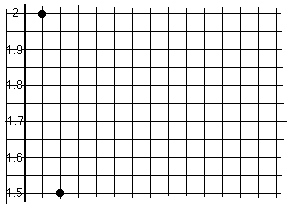
What do you notice? What is this sequence going to? This is a very
special number, can you find out what it is?
Write a program to get the ratios of successive Fibonacci numbers.
2. Looking at a regular pentagon:
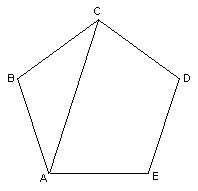 AC is a
diagonal of the regular pentagon. Draw in all the diagonals of the pentagon.
Label the points of intersections.
AC is a
diagonal of the regular pentagon. Draw in all the diagonals of the pentagon.
Label the points of intersections.
What do you see?
How many different size triangles are formed?
How many different size angles are formed?
Knowing that the sum of the angles of a triangle is 180 degrees, figure out the
number of degrees in each of the angles in the diagram.
How many different length segments are formed?
Measure all the lengths of the different segments (in mm.)
Find the ratio of bigger to smaller segments. What do you notice?
Some answers to problems from Ch. 7
For one reference, see "The Divine Proportion- a study in mathematical
beauty" by H. E. Huntley; Dover Publ.; 1970
See Xah Lee's spectacular site showing, of course, the equilateral spiral and
other curves!Xah Lee
To download
Don's materials
To choose sample problems from other chapters
Mathman home
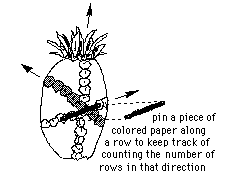 Buy a
pineapple. (This is one of those lessons that you can really eat up!) Look
carefully at the rows on it. There are three directions of rows. Count the rows
in each direction. This takes a while to see because every pineapple is not
perfect. If you are careful, you can do it! What do you find?
Buy a
pineapple. (This is one of those lessons that you can really eat up!) Look
carefully at the rows on it. There are three directions of rows. Count the rows
in each direction. This takes a while to see because every pineapple is not
perfect. If you are careful, you can do it! What do you find?

 AC is a
diagonal of the regular pentagon. Draw in all the diagonals of the pentagon.
Label the points of intersections.
AC is a
diagonal of the regular pentagon. Draw in all the diagonals of the pentagon.
Label the points of intersections.