Michael, a 5th grader, finds a Pattern in Infinite Series

After coloring squares for  -> 1 and -> 1/2 and 1/4+(1/4)^2+...-> 1/3, he came up with the generalization that 1/n + (1/n)^2 + (1/n)^3 + (1/n^4)' approaches the limit 1/(n-1).

Don showed Michael how to do this in Mathematica' and Derive. Michael  tried things to show how his rule works for big numbers..

The Greek symbol Sigma means sum. So this reads find the sum of 1/3 to the nth power as n goes from 1 to 2, to 3, ... to infinity and looks like this below

which approaches 1/2 as the limit.  Michael did the following:

-----------------------------------------------------

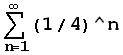
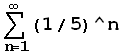
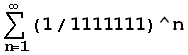
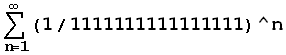
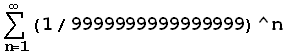
Don has found that many of his students try to see what happens when they push the envelope!

A week or two later, Don asked Michael to see what happens if we start with 2/5.

Michael did a number of infinite sums, starting with

2/5 , which went to 2/3 and

74/75,  which went to 74 and

7/676767677665883, which went to 7/676767677665876 and others,

and he figured out that

A/B + (A/B)^2 + (A/B)^3 + ' = A/(B-A)

He also found, by himself, that the infinite sum, starting with 89/6 gets bigger and bigger, it diverges. and starting with 3/3, the series would also diverge, does not approach a number. So they talked about how A and B were related.

 Michael said for the infinite geometric series to converge, 

A must be < B .

Fine work Michael!!!