James, age 9 from Tasmania, works in Don's worksheet book via his Math By Mail/Email & AIM

James' Mom, Carolyn, after looking at Don's worksheet book said, "The thing I liked best about Don's book is the way he encourages mistakes and alternative answers. We are very alternative".

From June 21:

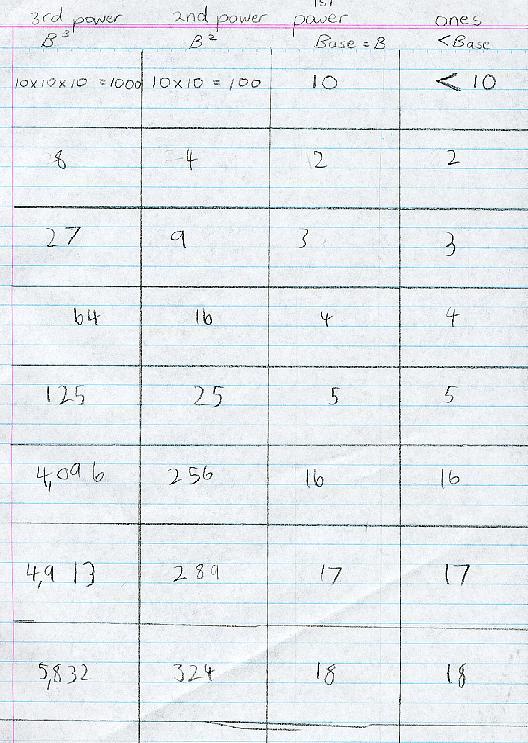
June 24, 2001 James was working on pp. 11-13 in Don's worksheet book and made a table of the place values in different bases (there should be a 1 in the ones column for every base). he scanned these sheets and sent them to Don as attached files. One he sent as an AIM file.

James made a code for writing numbers in base 5.

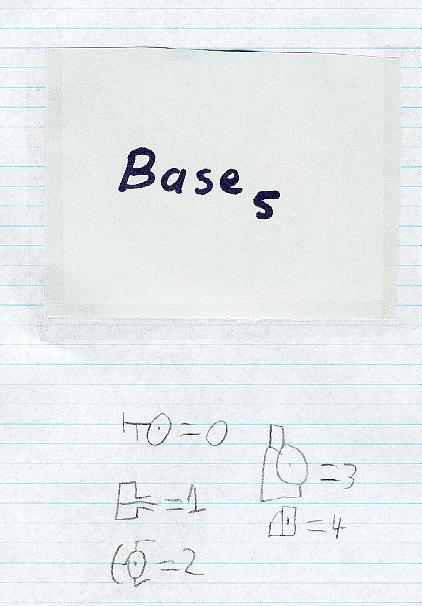
Then he sent Don the following problem to change the numeral in his base 5 code  to our base ten:

Don wrote this as 2100 (base 5) and equals 2x125 + 1x25 + 0x5 + 0x1 = 250 + 25 = 275 (base 10). And James over the voice using AIM told Don this was correct. Then Don gave James the following numeral in binary 11011 (base 2) to change to decimal. James came back quickly with 11011 (base 2) = 27 (base 10). Fine job James!

At this point in James' and Don's communications: James wants to do his work in Don's book first thing in the morning and Carolyn is very pleased with what James is doing.

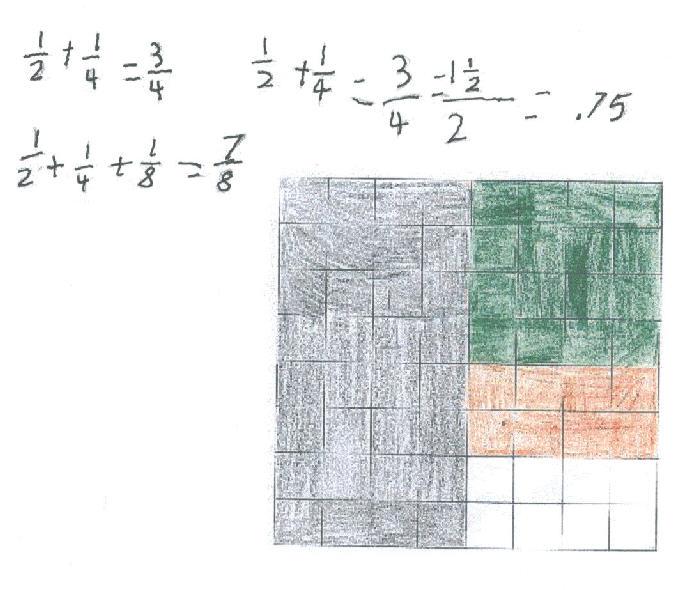
From James on July 11, 2001 after 2 weeks of bronchitis; his graph of the partial sums for 1/2 + 1/4 + 1/8 ...

July 19, 2001: Carolyn and Don had arranged this session by email. On AIM, James played the "Guess My Number" game with Don. James and his Mum had Don get Sheri's page on his screen. Then James asked Don which cards contained his number and he successfully found Don's number. Then Don found James' number. James graphed x+y=9 (because he is 9), scanned it and sent this to Don in AIM:

On AIM, Don had James find the coordinates for (10, -1) which he did and Don had him add  10  + -1 = 9 which he did. Don spent time talking with Carolyn about how the negatives should be written with the sign raised . Most textbooks after more than 30 years that we write it correctly, still write the negative number with a minus sign, then they need parentheses around it like 10 + (-1) = 9, and it gets very complicated. Don pointed this out to Carolyn on page 108 in his worksheet book, which they have near the computer. Carolyn communicated this to James. Then Don asked him to get the coordinates of a point between points on the graph. He found 2 1/2 and 6 1/2 and added them to get 9. Sometimes Don spoke to James and sometimes to his Mum, Carolyn.

Then James scanned and sent on AIM the table he extended for the "Guess My Rule" game on p. 87 in Ch. 6 of Don's worksheet book, which he figured out to be 2x+3=y. Don said he had a new rule for James to figure out.  (It was 3x-2=y) Don asked for a number to put into his machine. James said 100, Don gave him back 298. At that point James said Don's rule was 2x+98=y  because 2x100+98=298. Of course that works for his rule. Then Don asked James to try another number. He gave 10 and Don gave him back 28. There was dead silence for about a minute and James wrote 3x-2=y ! Don wrote YES! and James came back with YYYYYAAAAAAYYYYY!!! Everyone jumped with joy and clapped!  Don left 4 things for James to work on: 1/3 + 1/9 +... in Ch. 1, the cookie sharing in Ch. 2, graphing 2x+3=y on p. 92 in Ch. 6, and solving equations on p. 145 in Ch. 8. Despite the sound breaking up some, it was a very exciting session! Great work James!

July 26,'01 Hi Carolyn,

  My grandson (to be a father in March!) Aaron took the pictures of Tessa and I. I took the ones with Tessa and Terri, her Mom.

  My only comment on your thing with Michael was I wouldn't go to 800+800 too quickly. I stay with something they can do, 1+1, but change the size and names...like 1000000+1000000 and 1 sin x + 1 sin x.. Capice? Comprende? Dig? Next could be 1 square root of 7 + 1 square root of 7 (using the square root symbol),  -1 + -1 . At one point I think Tessa asked Michele what's 100,000 + 1,000,000 and I winced, and Michele answered correctly, but I don't think Tessa understood it. And I wouldn't do that! The kids always seem to make up harder ones than I do. I started a 5-year old here Tuesday and did a similar thing with her as I did with Tessa, and she did well also.

Have fun!

Cordially, Don

July 29, 01 Dear Don,
sorry no Idea what happened. The whole AIM thing dropped off and then refused to reconnect. it hooked up again ok after I shut down and rebooted.
Today ( friday ) I have to babysit friend's children ( she forgot the school is closed today ) so we can't be online - i'm taking them out to go cave exploring!

 james has done a bit more guess my rule, but he is still in go slow mode although the cough is much better thank you (change of medication).

That is such a lovely photo of you and Tessa - did Marilyn take it? I never thought of that as being important maths! little kids sure love doing this - Michael [age 5] and his little friend were helping me do the groceries and they're going "what's 2 plus two, what's 100 plus a 100, what's 800 plus 800 - 200 - no 800 is bigger than 200 so it can't be that - well what is it? - I don't know - 200 - but I know it's not 200" etc. till I can't concentrate on whether I wanted juice or milk.

cheers, Carolyn

July 29, 01  Dear Don
Hurray - James has finally had 2 days without a cough.
So renew us - he should be fine next week, but it might be best if he starts each chapter WITH you - he has tried writing a few equations today. today he wrote

1. 2*x + 8 = 24 + 10

2. 2*x + 8 = 34 + 10

3. 2*x + 4 = 44

he says that x=13 for number 1 but after I got really confused when he said the second equation didn't equal 44 it appears he probably meant

2*x + 8=24  then adding ten to get the next one

2*x + 8=34 then altering the other side by 4 while still stepping up by ten on the otherside?

2*x + 4=44
but now Michael is sick!
cheers,
Carolyn

Don talked with Carolyn about keeping the equations simple, like 2x+3=17 and referred her to p. 145, in ch.8 in his book.

August 2,  2001Hi Don,
my Aim is busy upgrading.

james was doing page 88 Guess my rule today. he also found an old series he did a few days ago and said it was "double it add 3" well how do you say that in mathematical language? "Two times, no - two ecks plus three equals Y. wow I didn't know I could say that!" so then he wrote the equations for 2 and 4, for the others he knows what is happening - number one is adding 7 to the y before, and he knows what number 3 looks like on a graph  but he can't express them.

I'll send the graph later

cheers, Carolyn
Carolyn sent James' graphs from p92 in Don's worksheet book.

August 3, 2001: James has been graphing equations in chapter 6 like 2x + 3 = y, and Carolyn wrote the following on AIM: ' I'm trying to say this is great - James has a new tool for visualizing equations/patterns. He can see mentally 'further' up and down the pattern with a graph than he can just with a table or an equation!' [Don says: That was the beauty of what Descartes did..he showed the relationship between the numbers in the table (the arithmetic) and the equation (the algebra) and the patterns in the points (the geometry)].

Don sent via AIM, 3 graphs for James to write the equations for:

August 8, '01 On AIM Carolyn told Don James had figured out the cards for The Magic Number game for base 3. On the original 5 cards in binary, they went up to 31 (1 less than 32, a power of 2). James thought going up to 26 (1 less than  27, a power of 3) would be too small, and 80 (1 less than 81, the next  power of 3) would be too large. He decided to go to 38. [One of Don's students on Aug. 13, ended up at 56 for the same problem!]

During this session on AIM, Don's students came in for class at that time. Amanda talked with Carolyn and the other student could hear her from Tasmania, on Don's speakers. Carolyn told us it was her birthday (it was Aug. 9, their time as we talked). We all sang Happy Birthday to her!

Then Don signed off for an hour to work with his students here. We he went back on AIM, this went on:

Carolyn: so really he's still having trouble writing equations to describe what he sees happening on the graph

[James then came on the microphone and the computer with AIM, and below is essentially the written conversation which was saved from AIM, with the oral conversation going on at the same time (which you can't see or hear)!]
Don: ok
Don: 2x+ ? = y
Don: crosses the y-axis at 0,7
James: 2x+7=y
Don: the equation is 2x+7=y
Don: right
James: but i still don't get it
Don: horizontal axis is x-axis
James: y=7?
Don: when x=0, y = 7
James: so 2x+7=7
James: 2x+7=y
Don: when x=0, y=7
James: ok
Don: when x=1, y=9 
James: 9 or 8?
forthferalz : 2
Don: 8 is right   [Don makes a mistake here!]
Don: sorry
James: so x-i,y=8 [James meant when x=1, y=8]
James: opps
Don: yes
James: ===========================
Don: when x=2, y=9
James: 9
Don: ok?
James: y is olways 7 more than x right?
Don: when x=2, y=11
James: you mean James [Don called James, Michael, his brother's name]
Don: 2x+7=y
James: yep
Don: when x=2 , 2x2+7=11
Don: when x=3, y=?
James: its two times x + 7=y
James: 13
James: ok
Don: ok
James: oatmeal??
Don: my brain is oatmeal
James: i eat that stuff
James: ib
James: ok
Don: that's 1b
Don: over 3 up 1
Don: the first number is 1/3
James: 1 over 3
Don: 1/3
James: 1 third
Don: is the first number
James: ok
Don: so the equation is 1/3 x + 5 = y
James: 1 third of x + 5 = y right?
Don: yes
James: okkkkkkkkkkkkkkkkkkkkkkkkkkkkk

9/6/01

Hi Don,

Can we stop for a fortnight?  They have school holidays next week. James did some stuff today. Sending it later. I would like to get into more of a routine where he does a tiny bit everyday and we chat online once a fortnight, or where he does a lot intensively for a few days once a month. He's quite slow and he has a lot of other 'regular' maths to learn too.

David is keen to do some stuff - he has tried the stuff on page 15 too but can't see how it goes to a half.

Carolyn

 

 

9/6/01

Dear Don,

late reply - OK? Have James start the quadratic equations. Did he find the equation for graph #3? [no]. Did he check graph #2? [no] Start on fibonacci numbers p129. [Maybe next month!]

How about starting with a 9 by 9 square on the graph paper and work on 1/3 +   1/3 of 1/3    +   1/3 of 1/3 of 1/3 ... (or 1/3 + 1/9 + 1/27...) [ok he's done that. but I'm pretty sure it's not all that clear to him what you want - at first he started colouring in a quarters of a squares by accident

- he didn't draw a nice obvious square outlined thickly in black and I think he just sort of got 'lost'. And he had some pretty strange answers for the questions initially. i'm not sure what he was thinking of. he thought the partial sums progress to one, then he thought it goes to 243.

 however he saw a pattern in the colouring in and cut out his shape and rearranged them to get oblongs stacking to the left and cubes stacking on the right. So we worked through it and it is clearer now i hope. using his graph he can see that if you draw a diagonal line that cuts from the top L corner to the bottom R and cut out the little end of the oblongs that stick over the line they fit next to the square of the next term and the whole series will never cross the halfway line.

 We haven't done a graph of x,y for it yet like Geoffrey but he seemed to know how to plot the points without any help, so he's started it.

cheers,Carolyn
might chat to you online tonight

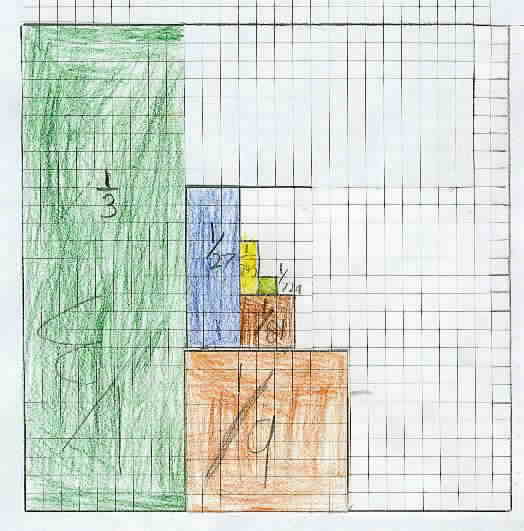
Notice the date written in the upper right corner was 6/9/01. That is the 6th day of the 9th month of the year 2001.

September 30, 2001

Carolyn sent Don James' graph below via AIM. Carolyn and Don talked about the patterns in the parabola, the curve, x*x=y.

Don suggested to Carolyn
1.) that James make his graphs so the origin (0,0) is not in the lower left corner so he could plot negative numbers for x.

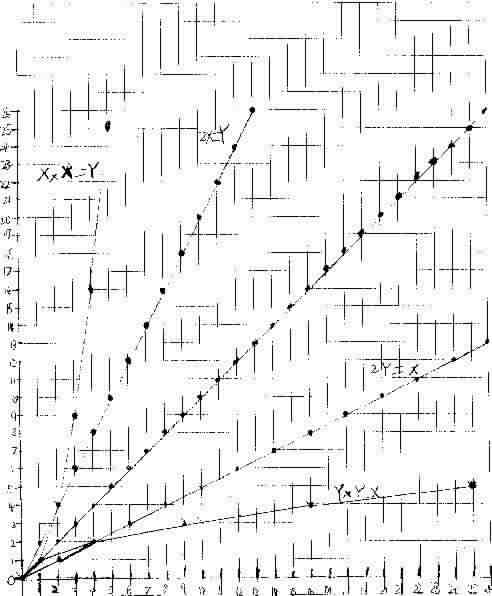
2.) The slope of the parabola changes, which makes it a curve, not a straight line when the slope is the same everywhere. Starting at (0,0), you go over 1 to the right and up 1 to get to the next (integral) point. From (1,1) you go1 to the right and 3 up. Then from (2,4) you go1 to the right and 3 up, then 5 up, then 7 up and so on. Why because 1+3=4=22 and 1+3+5=9=32 ,.., so the sum of the odd numbers is a square number- and x*x = x2 , a square.
3.) Don worked with James about multiplying negative numbers because Don wanted him to graph x*x=y when x= -3. So what is -3 x -3? Don used the pattern below from Sheri's page to help James get -3 x -3 = 9.

3.) It was James' idea to switch the x and y and graph y*y=x. That was a great idea James!
4.) Don worked with Carolyn on the differences in the y's, then the differences in the differences, which are all 2. The differences in consecutive odd numbers is 2. And the fact that the 2nd difference is constant, means the function is 2nd degree (x2).

 

To download Don's materials
Mathman home