
Continued & Infinite Continued Fractions/Chapter 8
Below is Grace's work on fractions to continued fractions, and continued fractions to fractions in Chapter 8:

Can you make a continued fraction equal to 27/8 ?
Make a continued fraction, then find the simplest fraction equal to it.
I gave Sara the continued fraction below; after a little thought, she said 3 1/5. It soon became clear to me that Sara didn't know how to divide fractions, which was the first thing she needed to do: 1 divided by 3 1/5. So instead of getting the answer to the original question, I worked on the division 1 divided by 1/2. To set the stage I asked her how many 4's make 12, or 12 ' 4, which she knew was 3. Then I had her do 1' ' = 2 = 2/1, 1' 1/3= 3..Then I gave her 1' 2/3 for which I drew the 1 cake and she showed me what 2/3 looked like and she figured out that there are 1 1/2 = 3/2 of the 2/3 in 1, so 1' 2/3 = 3/2. I told her the reciprocal of 2/3 is 3/2.

Then Sara made up the problem 9' 6/8 and she figured out this would equal 12. I showed her that for 9' 6/8, 1' 6/8 = 8/6, so 9' 6/8= 9x8/6 = 72/6 = 12 ( 9/1x8/6 = 72/6= 12) and this agrees with her answer. Sara was really excited about dividing fractions and multiplying she knew. We didn't finish the problem, but she learned how to divide fractions!
The next week, after a hug for Don, she finished the continued fraction, getting 3 16/37 !
Fine job Sara!
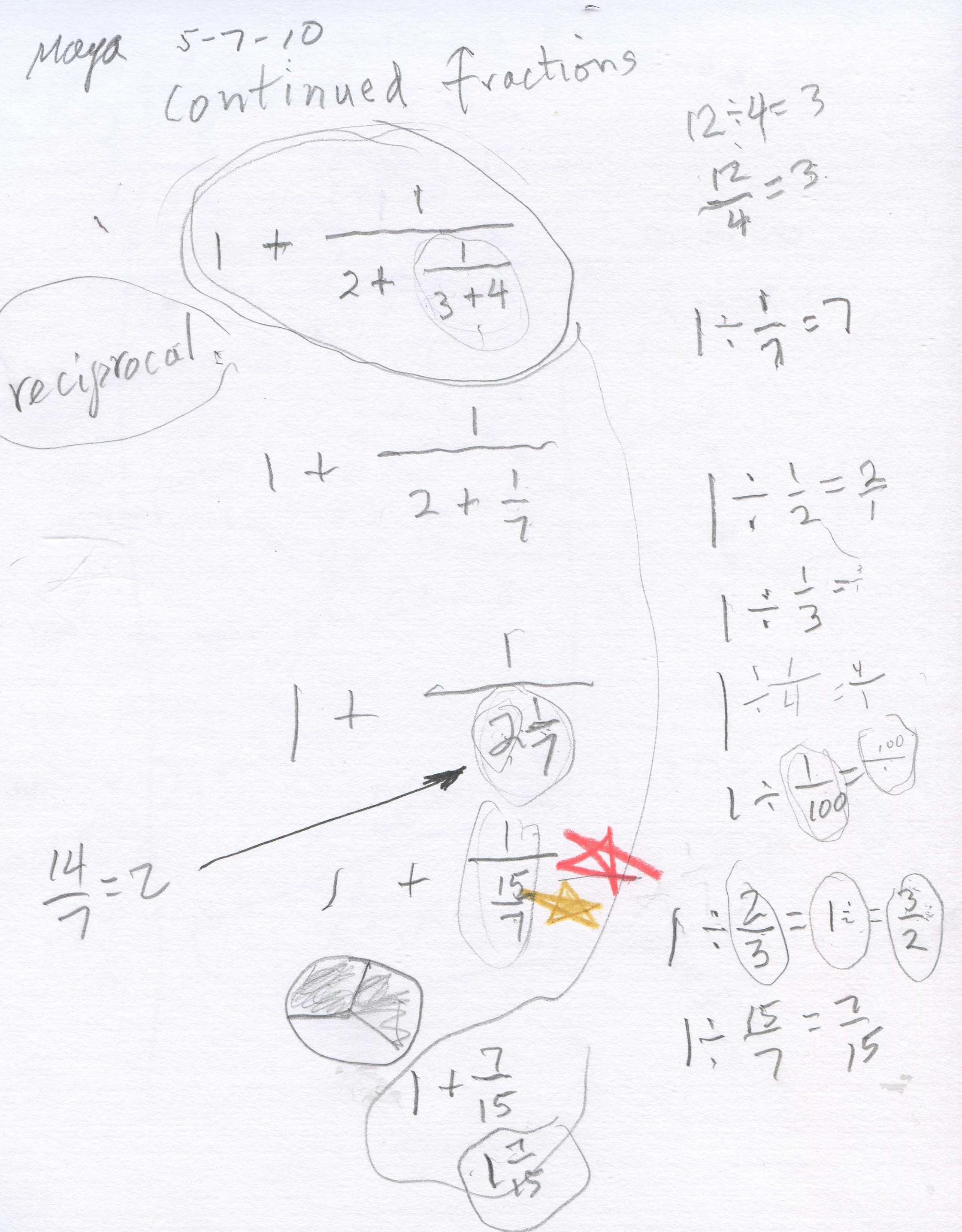
Maya knew that 2+1/7 = 15/7, then she did the rest, 1' 15/7 = 7/15, and she finished the problem with 1+7/15 = 1 7/15.
Fine job Maya!
We can solve the quadratic equation x2 -
5x + 6 = 0 to get x = ![]() .
.
We then take this function ![]() and in place of x we'll put
and in place of x we'll put
![]() , since this is equal to x, and we
get
, since this is equal to x, and we
get 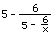 . Then we'll put
. Then we'll put
![]() in for x again, and we get
in for x again, and we get 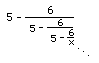 . If we keep doing that we get
an infinite
continued fraction. Jonathan, at age 7, did this at home with his Mom in CT,
using Don's original book. He got all excited about this being infinite! (He
came with his Dad for a week, in each of the next 2 summers).
. If we keep doing that we get
an infinite
continued fraction. Jonathan, at age 7, did this at home with his Mom in CT,
using Don's original book. He got all excited about this being infinite! (He
came with his Dad for a week, in each of the next 2 summers).
If you put 1 in the
first of these you get -1. If you put 1 in the second one you get 11. If
you put 1 in for x in the third one you get 4.4545.. You get an infinite
sequence which approaches 3, which is one of the two roots of the
original quadratic equation!
If
you start with -100, you would still get an infinite sequence approaching
3 as well. Notice, you only get the one root, 3, using this method #2
for solving the quadratic equation
x2
- 5x + 6 = 0.
Solving the same quadratic equation x2 - 5x + 6 = 0 by getting an infinite continued fraction- method #3:
Solve
for x another way to get:
x
= 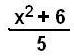
^2+6ov5.JPG)
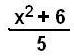
Solving the same quadratic equation x2 - 5x + 6 = 0 by getting an infinite continued fraction- method #4:
Solve for x another way to get:
x
=
then iterate
the right side to get
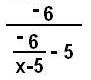
and so on to get an infinite continued fraction.
Iterating this same function -6/(x-5) in Mathematica using NestList, starting with 5, doing 1000 iterations, showing 250 digits, and looking at the last one, we get an infinite sequence that approaches 2, one of the roots of the original equation.
h[x_]:= -6/(x-5)
Take[N[NestList[h,5,1000],250],-1]
Power::infy: Infinite expression \[NoBreak]1/0\[NoBreak] encountered.
{1.99999999999999999999999999999999999999999999999999999999999
9999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999998784283
8015208649994273601205071405411499043769607328752211168623914688150}
Notice, when it uses 5, it gives "infinite expression encountered, then continues to do 999 more. I wondered what Mathematica did, so I started with 5 again, but only did 6 iterations and looked at all of them:
N[NestList[h,5,6],10]
Power::infy: Infinite expression \[NoBreak]1/0\[NoBreak] encountered.
{5.000000000,ComplexInfinity, 0,1.200000000,1.578947368,1.753846154,1.848341232}
Looking at the 6 numbers above, Mathematica showed the complexInfinity when 5 is put in for x, then put 0 in for x, and then continued on as if nothing happened. Hmmm.
Solve x2 - x -1 = 0 for an infinite continued fraction:
| We got the infinite continued fraction for ', the golden
mean, from the equation x2 - x -1 =
0 .
We added x and 1 to both sides to get x2
=
x + 1. Then we divided both sides by x
to get
for x on the right side, to get
|
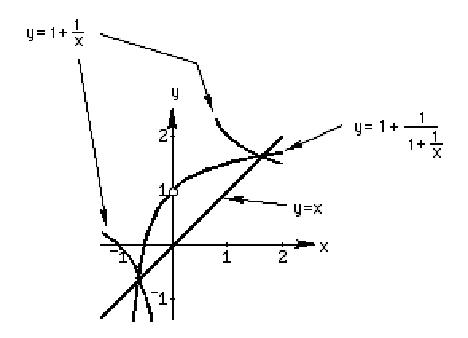 |
infinite continued fraction. On the way we graphed
,
and
.JPG)
Notice above, we are iterating the
function
The straight line and parts of 2 hyperbolas all intersect at the two points (1.618, 1.618) and ( -0.618, -0.618), which are the 2 solutions of the quadratic equation x2 - x -1 = 0 and are ' (the Golden Mean), and 1-' (see chapter 7). The infinite continued fraction for ' is:
| An infinite continued fraction for 4/p,
by Lord Brouncker, circa 1658--see Olds
|
An infinite continued fraction for e, see chapter
11), by Euler, circa 1737- see Olds:
|