The six trig functions and identities

The following diagrams are taken from the IES java applet in Japan at http://www.ies-math.com/math/java , a very important way of looking at all 6 trig functions at once. The color coding is the same as in the applet. Don uses these diagrams to get his students to show the relationships (make identities-equations that are true for all substitutions) between the 6 trig functions, expressing the tangent, cotangent, secant and cosecant in terms of the e and/or the cosine, the basis of all the trigonometric identities.

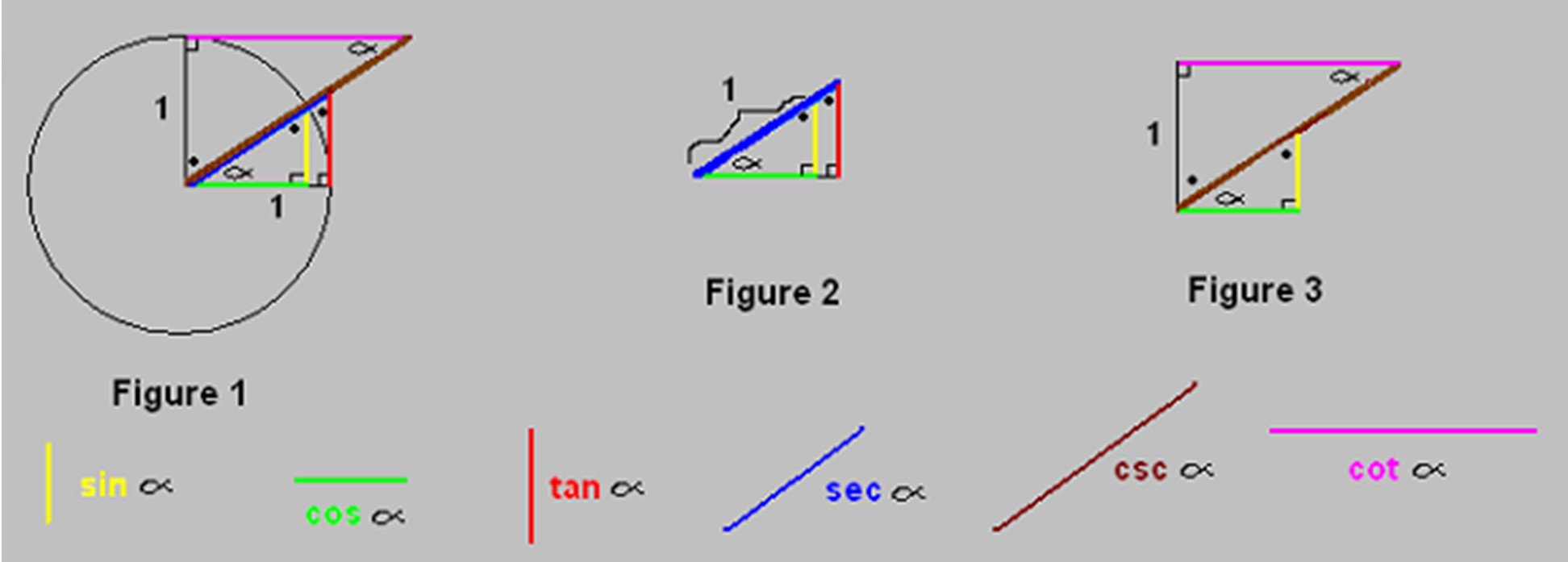
This will be done by using the three similar right triangles in Figure 1. The triangles are similar because their corresponding angles are equal (the [right] angles, the ' [dot] angles, and the (alpha) angles). In similar triangles, the corresponding sides are proportional. We will call the three triangles s (for small), m (for medium) and L (for Large). There are three things we have to keep track of in writing the proportions' one is which pair of triangles we are using, two, which pair of sides we are using, which are opposite the corresponding pair of angles.

We'll start by finding the tangent of , and go from the medium triangle to the small triangle in Figure 2:  

The proportion is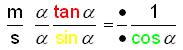

where

tells us we are going from the medium triangle to the small triangle.

tells us we are looking for the side opposite the  angle in the medium triangle-

(top) and opposite the  angle in the small triangle-

(bottom)

tells us we are looking for the side opposite the  angle in the medium triangle- 1

(top),  (which is the radius of the circle, 1) and the side opposite the   angle in the small 

triangle-

(bottom)

So 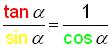 and multiplying both sides of the equation by , we get 

Identity #1.

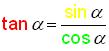
This is our first identity for trig, read as:

the tangent of alpha equals the sine of alpha divided by the cosine of alpha.

Now see if you can make up other proportions to get secant , cosecant , and cotangent  in terms of sin and/or cos . You will get

Identity #2. ,

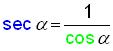Identity #3.  ,

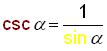Identity #4.

If you use other proportions, you can get other identities like .

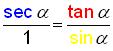Make sure you can do these yourself.

Other important identities can be obtained by using the Pythagorean theorem.

For example, in the small triangle, Identity #5 . In the medium triangle, Identity #6 and in the Large triangle, Identity #7 . Identity #6 can also be obtained from Identity #1 by dividing each term by  and the third of these identities can be obtained from

Identity #1 by dividing each term by .

Geoffrey, age 11 , sat at Don's computer using the IES page linked above, and graphed the 6 trig functions below:

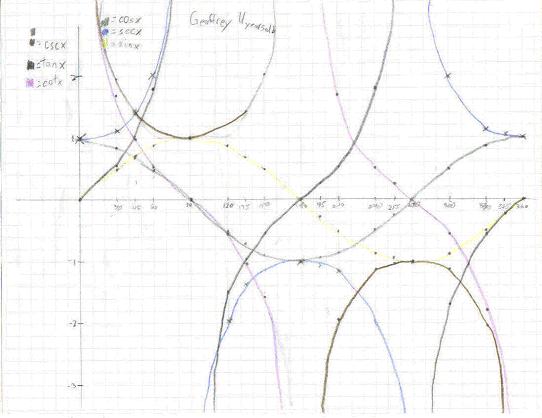
To order Don's materials
Mathman home