Area under curve 1/x -> logs, and the area under 1/(1+x) -> logs and infinite series/Chapter 13

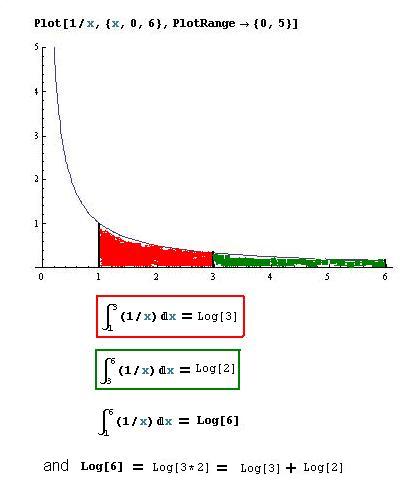
Don graphed 1/x in Mathematica and found the following:

The area under the curve 1/x from 1 to 3 is equal to the log_e 3 =~ 1.0986

The area under the curve 1/x from 3 to 6 is equal to the  log_e 2 =~ 0.6931

The area under the curve 1/x from 1 to 6 is equal to the  log_e 6 =~ 1.7917

The derivative of Log_ex = 1/x   -use the pencil approach, or

for a proof, see

 http://www.5min.com/Video/Learn-about-Proof-ddx--ln-x--1x-99173876

and the integral of 1/x = Log_ex

You might try other areas, like A_1-4 1/x  +  A_4-7 1/x  and see if it equals A_1-7  1/x .

Remember Ian's discovery in Ch. 3  1/(1-x) = (1-x)^-1 = 1+ x + x² + x³ + x⁴ + x⁵ +... 

   If we substitute ^-x in for x, we get  1/(1+x) = 1- x + x²  - x³  + x⁴  - x⁵  +...

Both of these series above converge for ^-1<x<1

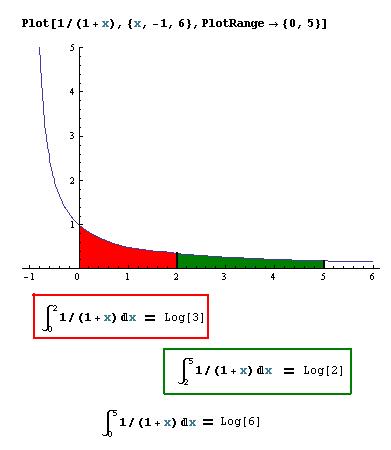
Don graphed 1/(x+1) in Mathematica and found the following:

The graph of  y = 1/(1+x)  at the right is part of an hyperbola like y = 1/x  except it is shifted 1 unit to the left. The area under this curve from from x = 0 to x = a or  A0-a 1/(1+x) = loge(1 + a) and if we use the generalizations from the section above, this will equal the integral of the infinite series 1 - a + a2 - a3 + a4 - a5 + ...  Taking the integral of each term separately, we get  A0-a 1/(1+x) = loge(1 + a) = a - a2/2 + a3/3 - a4/4 + a5/5 - a6/6 +' The natural log then, is the area under the curve  y=  1/x  or  y= 1/(1+x) and it is the infinite series loge(1 + a) = a - a2/2 + a3/3 - a4/4 + a5/5 - a6/6 +' CAUTION: you can't find the the loge(1 + 2) by

putting 2 in for a in the series above because this series converges only when a is between  ^-1 and 1. Newton found the logs of integers in a unique way. First he found the log_e 1.1 by putting .1 in for a in the series log_e(1 + .1) = .1 - (.1)²/2 + (.1)³/3 - (.1)⁴/4 + (.1)⁵/5 - (.1)⁶/6 +' = 0.0953, then similarly he got the logs of 1.2, 0.8 and 0.9. He then said  

2 = 1.2*1.2/(0.8*0.9). Who else would think of writing 2 this way! Newton then proceeded to get the log_e 2 by using the log identities log(A*B) = Log A + Log B and Log(C/D) = Log C - Log D: 

(check these identities that Kavi and Kevin found at logarithms )

then the log_e 2 = log_e(1 + 0.2) + log_e(1 + 0.2) - ((log_e(1 + ^-0.2) + log_e(1 + ^-0.1)). This reinforces, for me at least, that we have to write numbers different ways. Ever since I saw Sue Monell do "number names for todays date", everyday, with 5 and 6 year olds at Bank Street School for Children, 40 some years ago, I thought it was a great idea.

Write a program which will get this infinite series 

log_e(1 + a) = a - a²/2 + a³/3 - a⁴/4 + a⁵/5 - a⁶/6 +'

See if you can find log_e 3 and log_e 4 and others using Newton's method and check these on a calculator.